题目内容
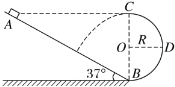
【题目】如图所示,半径为R的绝缘圆筒中有沿轴线方向的匀强磁场,磁场方向垂直纸面向里。从离子源产生的甲、乙两种正离子,经加速电压加速后从M点垂直于磁场射入匀强磁场,正离子与筒壁的碰撞是弹性碰撞(碰撞时无能量和电荷量损失),最终都从M点射出磁场。已知甲离子的质量为m,电荷量为q, 与筒壁碰撞了2次;乙离子与筒壁碰撞了3次。不计离子的重力和相互作用,正离子由离子源飞出时的速度可忽略不计。求:

(1)甲、乙离子在磁场中运动的半径之比;
(2)加速电压U与磁感应强度B之间满足的关系式和乙离子的比荷。
【答案】(1)![]() (2)
(2)![]() ;
;![]()
【解析】
(1)甲离子与筒壁碰撞了2次,其轨迹把圆筒三等分,如图所示,根据几何关系得
tan60°=![]()

同理可得乙离子的轨迹半径应满足
tan45°=![]()
所以甲、乙离子在磁场中运动的半径之比为
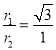
(2)设加速电压为U,匀强磁场的磁感应强度为B,对甲离子利用动能定理得
qU= ![]()
根据牛顿第二定律得
![]()
解得
![]()
同理,对乙离子利用动能定理得
q2U= ![]()
根据牛顿第二定律得
![]()
解得
![]()

练习册系列答案
相关题目