题目内容
1．以速度v0水平抛出一个质量为1kg的物体，若在抛出2s后它未与地面及其他物体相碰，则它在2s内的动量的变化大小为20kgm/s方向为竖直向下．分析 根据动量定理，结合合力的冲量求出动量的变化量大小和方向．
解答 解：根据动能定理知，2s内动量的变化量△p=mgt=10×2kgm/s=20kgm/s，方向竖直向下．
故答案为：20kgm/s，竖直向下．
点评 解决本题的关键知道合力的冲量等于动量的变化量，合力冲量的方向与动量变化量的方向相同．
练习册系列答案
相关题目
12．
如图所示，竖直平面内放一直角杆AOB，杆的水平部分粗糙，动摩擦因数为0.20，杆的竖直部分光滑，两部分各套有质量分别为2.0kg和1.0kg的小球A和B，A、B间用细绳相连，初始位置OA=1.5m，OB=2.0m，g取10m/s2，则若用水平拉力F1沿杆向右缓慢拉A，使之移动0.5m，该过程中拉力F1做功（ ）
如图所示，竖直平面内放一直角杆AOB，杆的水平部分粗糙，动摩擦因数为0.20，杆的竖直部分光滑，两部分各套有质量分别为2.0kg和1.0kg的小球A和B，A、B间用细绳相连，初始位置OA=1.5m，OB=2.0m，g取10m/s2，则若用水平拉力F1沿杆向右缓慢拉A，使之移动0.5m，该过程中拉力F1做功（ ）| A． | 3.0J | B． | 8.0J | C． | 0 | D． | 5.0J |
9．
如图所示，光滑斜面倾角为θ，c为斜面上的固定挡板．物块a和b通过轻质弹簧连接，a，b处于静止状态，弹簧压缩量为x．现对a施加沿斜面向下的外力使弹簧再压缩3x，之后突然撤去外力，经时间t，物块a沿斜面向上运动的速度为v，此时物块b刚要离开挡板．已知两物块的质量均为m，重力加速度为g．下列说法正确的是（ ）
如图所示，光滑斜面倾角为θ，c为斜面上的固定挡板．物块a和b通过轻质弹簧连接，a，b处于静止状态，弹簧压缩量为x．现对a施加沿斜面向下的外力使弹簧再压缩3x，之后突然撤去外力，经时间t，物块a沿斜面向上运动的速度为v，此时物块b刚要离开挡板．已知两物块的质量均为m，重力加速度为g．下列说法正确的是（ ）| A． | 弹簧的劲度系数为$\frac{mgsinθ}{2x}$ | |
| B． | 物块b刚要离开挡板时，a的加速度为gsinθ | |
| C． | 撤去外力后，经过时间t，弹簧弹力对物块a做的功为5mgxsinθ+$\frac{1}{2}$mv2 | |
| D． | 物块a沿斜面向上运动速度最大时，物块b对挡板c的压力为O |
16．
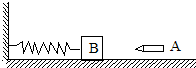如图所示，轻弹簧与木块连接另一端固定在竖直的墙壁上，木块B放于光滑水平面上，弹簧处原长状态，一颗子弹A以水平速度射入木块内（此过程时间非常短），将弹簧压缩到最短，将子弹、木块、弹簧作为系统，则此系统在从子弹接触木块开始到弹簧被压缩至最短的过程中，下列说法中不正确的是（ ）
如图所示，轻弹簧与木块连接另一端固定在竖直的墙壁上，木块B放于光滑水平面上，弹簧处原长状态，一颗子弹A以水平速度射入木块内（此过程时间非常短），将弹簧压缩到最短，将子弹、木块、弹簧作为系统，则此系统在从子弹接触木块开始到弹簧被压缩至最短的过程中，下列说法中不正确的是（ ）| A． | 动量守恒，机械能守恒 | B． | 动量不守恒，机械能不守恒 | ||
| C． | 动量守恒，机械能不守恒 | D． | 动量不守恒，机械能守恒 |
6．下列关于质点概念的说法中，正确的是（ ）
| A． | 任何细小的物体都可以看作质点 | |
| B． | 任何静止的物体都可看作质点 | |
| C． | 一个物体是否可以看作质点，要看所研究问题的具体情况而定 | |
| D． | 一个物体在某种情况下可看作质点，那么在任何情况下都可看作质点 |
如图质量为m=1kg的小球乙静止在光滑的水平面上，质量同为m=1kg的小球甲以初速度V0水平向右运动并在A点与乙发生弹性碰撞，碰后小球乙进入半径R=0.4m的光滑半圆形轨道，并恰能通过轨道的最高点B．求 （g=10m/s2）
11．
如图所示为一个做匀变速曲线运动的质点的轨迹示意图，已知在B点的速度与加速度相互垂直，则下列说法中正确的是（ ）
如图所示为一个做匀变速曲线运动的质点的轨迹示意图，已知在B点的速度与加速度相互垂直，则下列说法中正确的是（ ）| A． | D点的速率比C点的速率大 | |
| B． | A点的加速度与速度的夹角小于90° | |
| C． | A点的加速度比D点的加速度大 | |
| D． | 从A到D加速度与速度的夹角先增大后减小 |