题目内容
如图所示，光滑半圆形轨道处于竖直平面内，半圆轨道与光滑的水平地面相切于半圆的端点A。一质量为m的小球在水平地面上的C点受水平向左的恒力F由静止开始运动，当运动到A点时撤去恒力F，小球沿竖直半圆轨道运动到轨道最高点B点，最后又落在水平地面上的D点（图中未画出）。已知A、C间的距离为L,重力加速度为g。
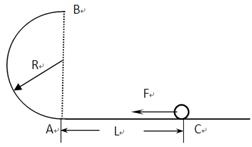
（1）若轨道半径为R，求小球到达圆轨道B点时对轨道的压力FN;
（2）为使小球能运动到轨道最高点B，求轨道半径的最大值Rm；
（3）轨道半径R多大时，小球在水平地面上的落点D到A点的距离最大？最大距离xm是多少？
（1）若轨道半径为R，求小球到达圆轨道B点时对轨道的压力FN;
（2）为使小球能运动到轨道最高点B，求轨道半径的最大值Rm；
（3）轨道半径R多大时，小球在水平地面上的落点D到A点的距离最大？最大距离xm是多少？
（1）
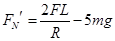，方向竖直向上 （2）
（3）
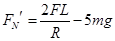，方向竖直向上 （2） （3） 试题分析：（1）设小球到达B点时速度为
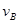，根据动能定理有
设B点时轨道对小球的压力为
，对小球在B点时进行受力分析如图，则有
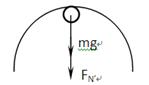
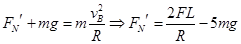
根据牛顿第三定律可知小球对轨道的压力
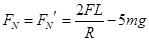，方向竖直向上（2）小球能够到达最高点的条件是
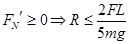
故轨道半径的最大值
（3）从B点飞出后做平抛运动，落地时间
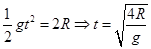
D到A的距离
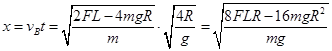
相当于二次函数求最大值的问题，最大值在
时取到（因为
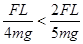，所以最大值可以取得到）代入
，得到此时最大距离点评：小球在最高点时合外力等于向心力，过最高点的临界条件是小球对轨道的压力为零，即重力等于向心力。
练习册系列答案
相关题目
和B´，使油滴恰好不碰到a板，且沿原路与细管无接触地返回并穿过M孔，请给出
，质量m=10g的绝缘物块，物体与水平面动摩擦因数μ=0.2，沿x轴正方向给物块一个初速度v0=2m/s，如图10，求：(g取10m/s2)
的小球以
的速度与质量为
的静止小球正碰，关于碰后速度
与
，下面可能的是
，
，
，
的水平速度抛出。