题目内容
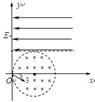
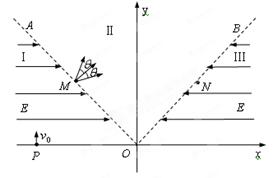
如图所示为某一仪器的部分原理示意图,虚线OA、OB关于y轴对称,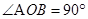 , OA、OB将xOy平面分为Ⅰ、Ⅱ、Ⅲ三个区域,区域Ⅰ、Ⅲ内存在水平方向的匀强电场,电场强度大小相等、方向相反。质量为m电荷量为q的带电粒子自x轴上的粒子源P处以速度v0沿y轴正方向射出,经一定时间到达OA上的M点,且此时速度与OA垂直。已知M到原点O的距离OM = L,不计粒子的重力。求:
, OA、OB将xOy平面分为Ⅰ、Ⅱ、Ⅲ三个区域,区域Ⅰ、Ⅲ内存在水平方向的匀强电场,电场强度大小相等、方向相反。质量为m电荷量为q的带电粒子自x轴上的粒子源P处以速度v0沿y轴正方向射出,经一定时间到达OA上的M点,且此时速度与OA垂直。已知M到原点O的距离OM = L,不计粒子的重力。求:
(1)匀强电场的电场强度E的大小;
(2)为使粒子能从M点经Ⅱ区域通过OB上的N点,M、N点关于y轴对称,可在区域Ⅱ内适当范围加一垂直xOy平面的匀强磁场,求该磁场的磁感应强度的最小值和粒子经过区域Ⅲ到达x轴上Q点的横坐标;
(3)当匀强磁场的磁感应强度取(2)问中的最小值时,且该磁场仅分布在一个圆形区域内。由于某种原因的影响,粒子经过M点时的速度并不严格与OA垂直,成散射状,散射角为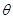 (
(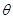 较小),但速度大小均相同,如图所示,求所有粒子经过OB时的区域长度。
较小),但速度大小均相同,如图所示,求所有粒子经过OB时的区域长度。
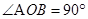 , OA、OB将xOy平面分为Ⅰ、Ⅱ、Ⅲ三个区域,区域Ⅰ、Ⅲ内存在水平方向的匀强电场,电场强度大小相等、方向相反。质量为m电荷量为q的带电粒子自x轴上的粒子源P处以速度v0沿y轴正方向射出,经一定时间到达OA上的M点,且此时速度与OA垂直。已知M到原点O的距离OM = L,不计粒子的重力。求:
, OA、OB将xOy平面分为Ⅰ、Ⅱ、Ⅲ三个区域,区域Ⅰ、Ⅲ内存在水平方向的匀强电场,电场强度大小相等、方向相反。质量为m电荷量为q的带电粒子自x轴上的粒子源P处以速度v0沿y轴正方向射出,经一定时间到达OA上的M点,且此时速度与OA垂直。已知M到原点O的距离OM = L,不计粒子的重力。求:
(1)匀强电场的电场强度E的大小;
(2)为使粒子能从M点经Ⅱ区域通过OB上的N点,M、N点关于y轴对称,可在区域Ⅱ内适当范围加一垂直xOy平面的匀强磁场,求该磁场的磁感应强度的最小值和粒子经过区域Ⅲ到达x轴上Q点的横坐标;
(3)当匀强磁场的磁感应强度取(2)问中的最小值时,且该磁场仅分布在一个圆形区域内。由于某种原因的影响,粒子经过M点时的速度并不严格与OA垂直,成散射状,散射角为
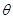 (
(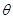 较小),但速度大小均相同,如图所示,求所有粒子经过OB时的区域长度。
较小),但速度大小均相同,如图所示,求所有粒子经过OB时的区域长度。(1)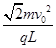 (2)
(2)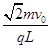
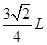 (3)2Lsinθ
(3)2Lsinθ
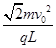 (2)
(2)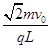
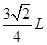 (3)2Lsinθ
(3)2Lsinθ试题分析:(1)粒子在Ⅰ区域内做类平抛运动,

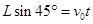
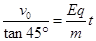
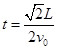
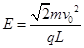
(2) 粒子在Ⅱ区域内做匀速圆周运动,其轨道半径
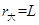
因为
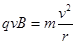 又
又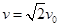
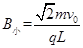
粒子进入Ⅲ区域后,其运动轨迹NQ与PM对称,则
水平位移
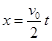
由(1)知:
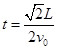
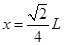
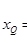
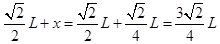
(3)该圆形磁场区域的半径r等于其轨迹圆半径R,即r=R=L
所有粒子出磁场时速度方向平行,其落点在直线OB上的GH两点之间,如图
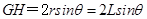
点评:如果组合场是电场和磁场组合则带电粒子在电场中做类平抛会匀变速直线运动,类平抛分解成匀速直线运动和初速度为零的匀加速直线运动来研究;在磁场中做匀速圆周运动,洛伦兹力为向心力,根据几何关系找半径,根据圆心角求时间。

练习册系列答案
相关题目

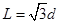 ,两板间所加电压为U,D板的右侧边缘恰好是倾斜挡板NM上的一个小孔K,NM与水平挡板NP成
,两板间所加电压为U,D板的右侧边缘恰好是倾斜挡板NM上的一个小孔K,NM与水平挡板NP成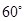 角,且挡板足够长,K与N间的距离为
角,且挡板足够长,K与N间的距离为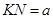 .现有一质量为m、电荷量为q的带正电的粒子,从A、D的中点O沿平行于金属板方向
.现有一质量为m、电荷量为q的带正电的粒子,从A、D的中点O沿平行于金属板方向 以某一速度射入,不计粒子的重力.该粒子穿过金属板后恰好穿过小孔K:
以某一速度射入,不计粒子的重力.该粒子穿过金属板后恰好穿过小孔K: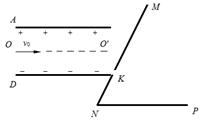
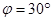 ,A点与原点0的距离为d.接着,质点进入磁场,并垂直丁OC飞离磁场。不计重力影响。若OC与x轴的夹角也为φ.
,A点与原点0的距离为d.接着,质点进入磁场,并垂直丁OC飞离磁场。不计重力影响。若OC与x轴的夹角也为φ.