题目内容
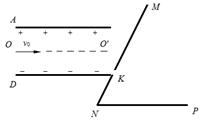
(15分)如图所示,水平放置的平行金属板A和D间的距离为d,金属板长为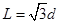 ,两板间所加电压为U,D板的右侧边缘恰好是倾斜挡板NM上的一个小孔K,NM与水平挡板NP成
,两板间所加电压为U,D板的右侧边缘恰好是倾斜挡板NM上的一个小孔K,NM与水平挡板NP成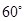 角,且挡板足够长,K与N间的距离为
角,且挡板足够长,K与N间的距离为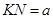 .现有一质量为m、电荷量为q的带正电的粒子,从A、D的中点O沿平行于金属板方向
.现有一质量为m、电荷量为q的带正电的粒子,从A、D的中点O沿平行于金属板方向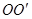 以某一速度射入,不计粒子的重力.该粒子穿过金属板后恰好穿过小孔K:
以某一速度射入,不计粒子的重力.该粒子穿过金属板后恰好穿过小孔K:
(1)求该粒子从O点射入时的速度大小v0;
(2)若两档板所夹的整个区域存在一垂直纸面向外的匀强磁场,粒子经过磁场偏转后能垂直打在水平挡板NP上,求该磁场的磁感应强度的大小B0;
(3)若磁场方向变为垂直纸面向里,且只存在于两档板所夹间的某一区域内,同样使该粒子经过磁场偏转后能垂直打在水平挡板NP上(之前与挡板没有碰撞),求满足条件的磁感应强度的最小值Bmin.
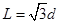 ,两板间所加电压为U,D板的右侧边缘恰好是倾斜挡板NM上的一个小孔K,NM与水平挡板NP成
,两板间所加电压为U,D板的右侧边缘恰好是倾斜挡板NM上的一个小孔K,NM与水平挡板NP成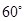 角,且挡板足够长,K与N间的距离为
角,且挡板足够长,K与N间的距离为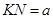 .现有一质量为m、电荷量为q的带正电的粒子,从A、D的中点O沿平行于金属板方向
.现有一质量为m、电荷量为q的带正电的粒子,从A、D的中点O沿平行于金属板方向 以某一速度射入,不计粒子的重力.该粒子穿过金属板后恰好穿过小孔K:
以某一速度射入,不计粒子的重力.该粒子穿过金属板后恰好穿过小孔K:
(1)求该粒子从O点射入时的速度大小v0;
(2)若两档板所夹的整个区域存在一垂直纸面向外的匀强磁场,粒子经过磁场偏转后能垂直打在水平挡板NP上,求该磁场的磁感应强度的大小B0;
(3)若磁场方向变为垂直纸面向里,且只存在于两档板所夹间的某一区域内,同样使该粒子经过磁场偏转后能垂直打在水平挡板NP上(之前与挡板没有碰撞),求满足条件的磁感应强度的最小值Bmin.
(1)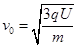 (2)
(2)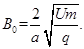 (3)
(3)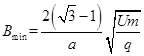
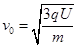 (2)
(2)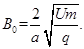 (3)
(3)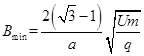
试题分析:(1)粒子在电场中做类平抛运动:
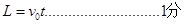


代入
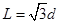 可得:
可得: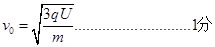
(2)射入的粒子在进入K时竖直方向的分速度为
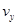
水平方向:
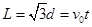
竖直方向:
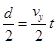
可得:
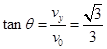 即:
即: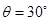 ,粒子垂直MN板入射………………….2.分
,粒子垂直MN板入射………………….2.分粒子到达K点时速度为:
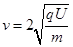 ……………………….1分
……………………….1分由几何关系可得:粒子圆周运动半径为
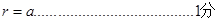
且满足:
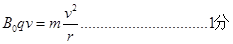
可得:

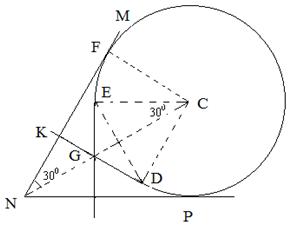
(3)磁场反向,如图,粒子从K点入射后做匀速直线运动从D点开始进入磁场,根据对称性,需偏转300o后从E点射出,做匀速直线运动垂直打到NP挡板上。
根据:
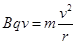 可得:
可得: 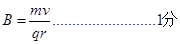
要使B最小,则需使半径r最大,临界情况是轨迹刚好和挡板相切………………………..1分
由几何关系可得:
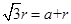 可得:
可得: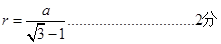
解得:
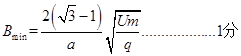
点评:难度较大,涉及到的运动过程较多,首先分析粒子的受力过程,在分析物体的运动过程,求解交叉点的速度大小以及方向,详细确定粒子的运动轨迹,把整段过程分解,逐个过程列公式分析

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
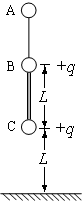
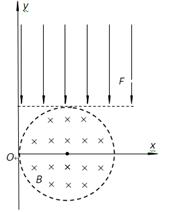
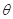 = 300角的斜向下直线做匀速运动,经过y轴上的B点进入x<0的区域,要使小球进入x<0区域后能在竖直面内做匀速圆周运动,需在x<0区域另加一匀强电场,若带电小球做圆周运动通过x轴上的C点,且
= 300角的斜向下直线做匀速运动,经过y轴上的B点进入x<0的区域,要使小球进入x<0区域后能在竖直面内做匀速圆周运动,需在x<0区域另加一匀强电场,若带电小球做圆周运动通过x轴上的C点,且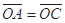 ,设重力加速度为g,
,设重力加速度为g,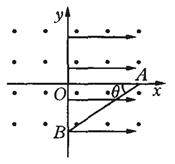
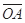 的长度.
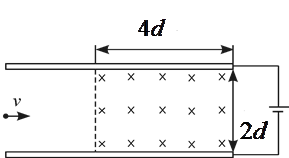
的长度.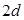 的长金属板接在电压可调的电源上。两板之间的右侧长度为
的长金属板接在电压可调的电源上。两板之间的右侧长度为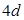 的区域存在方向垂直纸面向里的匀强磁场,磁感应强度为
的区域存在方向垂直纸面向里的匀强磁场,磁感应强度为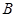 。喷墨打印机的喷口可在两极板左侧上下自由移动,并且从喷口连续不断喷出质量均为
。喷墨打印机的喷口可在两极板左侧上下自由移动,并且从喷口连续不断喷出质量均为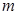 、速度水平且大小相等、带等量电荷的墨滴。调节电源电压至
、速度水平且大小相等、带等量电荷的墨滴。调节电源电压至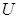 ,使墨滴在电场的左侧区域恰能沿水平方向向右做匀速直线运动。(重力加速度为
,使墨滴在电场的左侧区域恰能沿水平方向向右做匀速直线运动。(重力加速度为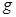 )
)

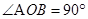 , OA、OB将xOy平面分为Ⅰ、Ⅱ、Ⅲ三个区域,区域Ⅰ、Ⅲ内存在水平方向的匀强电场,电场强度大小相等、方向相反。质量为m电荷量为q的带电粒子自x轴上的粒子源P处以速度v0沿y轴正方向射出,经一定时间到达OA上的M点,且此时速度与OA垂直。已知M到原点O的距离OM = L,不计粒子的重力。求:
, OA、OB将xOy平面分为Ⅰ、Ⅱ、Ⅲ三个区域,区域Ⅰ、Ⅲ内存在水平方向的匀强电场,电场强度大小相等、方向相反。质量为m电荷量为q的带电粒子自x轴上的粒子源P处以速度v0沿y轴正方向射出,经一定时间到达OA上的M点,且此时速度与OA垂直。已知M到原点O的距离OM = L,不计粒子的重力。求: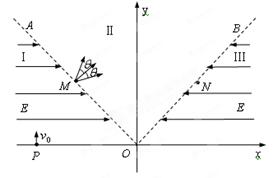
 (
(