题目内容
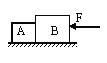
【题目】如图所示,小车上放着由轻弹簧连接的质量为mA=1 kg、mB=0.5 kg的A、B两物体,两物体与小车间的最大静摩擦力分别为4 N和1 N,弹簧的劲度系数k=0.2 N/cm。
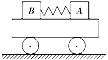
(1)为保证两物体随车一起向右加速运动,弹簧的最大伸长是多少厘米?
(2)为使两物体随车一起向右以最大的加速度向右加速运动,弹簧的伸长是多少厘米?
【答案】(1)10 cm(2)3.33m
【解析】
(1)为保证两物体随车一起向右加速运动,而且弹簧的伸长量最大,A、B两物体所受静摩擦力应达到最大,方向分别向右、向左.先根据牛顿第二定律求出整体的加速度,再隔离A列出方程,求解即可.
(2)为使两物体随车一起向右以最大的加速度向右加速运动,A、B两物体所受静摩擦力应达到最大,方向均向右.先对整体后隔离A,运用牛顿第二定律求解。
(1)为保证两物体随车一起向右加速运动,且弹簧的伸长量最大,A、B两物体所受静摩擦力应达到最大,方向分别向右、向左。对A、B作为整体应用牛顿第二定律![]() ,对A应用牛顿第二定律FfA-kx=mAa解得x=10 cm。
,对A应用牛顿第二定律FfA-kx=mAa解得x=10 cm。
(2)为使两物体随车一起向右以最大的加速度向右加速运动,A、B两物体所受静摩擦力应达到最大,方向均向右。对A、B作为整体应用牛顿第二定律a=![]() =
=![]() m/s2
m/s2
对A应用牛顿第二定律FfA-kx=mAa解得x≈3.33 cm。

练习册系列答案
相关题目