题目内容
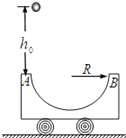
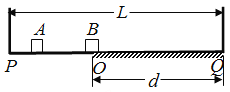
【题目】如图所示,底端切线水平且竖直放置的光滑![]() 圆弧轨道的半径为R=2m,其轨道底端P距地面的高度为h=5m,P与右侧竖直墙的距离为L=1.8m,Q为圆弧轨道上的一点,它与圆心O的连线OQ与竖直方向的夹角为53°.现将一质量为m=100g、可视为质点的小球从Q点由静止释放,重力加速度g=10m/s2,不计空气阻力。(sin53°=0.8,cos53°=0.6)试求:
圆弧轨道的半径为R=2m,其轨道底端P距地面的高度为h=5m,P与右侧竖直墙的距离为L=1.8m,Q为圆弧轨道上的一点,它与圆心O的连线OQ与竖直方向的夹角为53°.现将一质量为m=100g、可视为质点的小球从Q点由静止释放,重力加速度g=10m/s2,不计空气阻力。(sin53°=0.8,cos53°=0.6)试求:

(1)小球运动到P点时对轨道的压力多大;
(2)若小球每次和竖直墙壁的碰撞均是弹性碰撞,则小球的最终落地点离右侧墙角B点的距离。(小球和地面碰撞后不再弹起)
【答案】(1) ![]() (2)
(2) ![]()
【解析】(1)小球由Q到P的过程,由动能定理可得![]() ①
①
在P点小球所受的支持力为F,由牛顿第二定律有![]() ②,
②,
联立①②两式解得F=1.8N,根据牛顿第三定律可知,小球对轨道的压力大小为1.8N
(2)小球到达P点时速度的大小为v,由①可得v=4m/s④
若右侧无墙壁,则小球做平抛运动的时间![]() ⑤
⑤
联立④⑤解得小球做平抛运动的射程x=vt=4cm
由弹性碰撞和镜面对称的规律可知,小球和左右两侧竖直墙壁各碰一次后,落到地面上,落点与B点相距![]()
点睛:本题考查了动能定理和平抛运动,圆周运动的综合应用,知道平抛运动在水平方向和竖直方向上的运动规律以及圆周运动向心力得来源是解决本题的关键。
【题型】解答题
【结束】
11
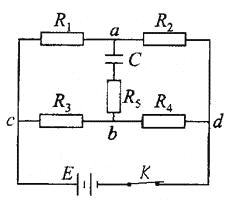
【题目】如图所示,相距L=0.5m的平行导轨MNS、PQT处在磁感应强度B=0.4T的匀强磁场中,水平导轨处的磁场方向竖直向上,光滑倾斜导轨处的磁场方向垂直于导轨平面斜向下,质量均为m=40g,电阻均为R=0.1Ω的导体棒ab、cd均垂直放置于导轨上,并与导轨接触良好,导轨电阻不计。质量为M=200g的物体C,用绝缘细线绕 过光滑的定滑轮分别与导体棒ab、cd相连接,细线沿导轨中心线且在导轨平面内,细线与滑轮质量不计,已知倾斜导轨与水平面的夹角θ=37°,水平导轨与ab棒间的动摩擦因数μ=0.4,重力加速度![]() ,水平导轨足够长,导体棒cd运动中始终不离开倾斜导轨,物体C由静止释放,当它达到最大速度时下落高度h=1m,试求这一运动过程中:(
,水平导轨足够长,导体棒cd运动中始终不离开倾斜导轨,物体C由静止释放,当它达到最大速度时下落高度h=1m,试求这一运动过程中:(![]() ):
):

(1)物体C能达到的最大速度![]() ;
;
(2)系统产生的内能是多少?
(3)连接cd棒的细线对cd棒做的功是多少?
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】(1)设C达到最大速度为![]() ,由法拉第电磁感应定律可得回路的感应电动势为
,由法拉第电磁感应定律可得回路的感应电动势为![]() ①
①
由欧姆定律可得回路中的电流强度为![]() ②
②
金属导体棒ab、cd受到的安培力为F=BIL③
线中张力为![]() ,导体棒ab、cd及物体C的受力如图,
,导体棒ab、cd及物体C的受力如图,
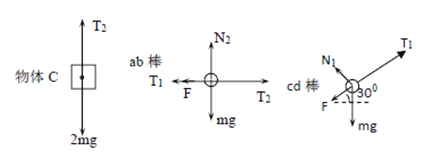
由平衡条件可得:
![]() ④
④
联立①②③④解得![]()
(2)系统在该过程中产生的内能为![]() ,由能的转化和守恒定律可得
,由能的转化和守恒定律可得![]() ⑥,联立⑤⑥将h=1m代入可得
⑥,联立⑤⑥将h=1m代入可得![]() ⑦
⑦
(3)运动过程中由于摩擦产生的内能![]()
由第二问的计算结果可知,这一过程由电流产生的内能![]()
又因为ab棒、cd棒的电阻相等,故电流通过cd棒产生的内能![]()
对导体棒cd,设这一过程中细线对其做的功为W,则由能的转化和守恒定律可得![]() ⑧
⑧
联立⑤⑦⑧可得W=0.84J

 阅读快车系列答案
阅读快车系列答案