题目内容
【题目】如图所示,质量为m的半圆轨道小车静止在光滑的水平地面上,其水平直径AB长度为2R,现将质量也为m的小球从距A点正上方h0高处由静止释放,然后由A点经过半圆轨道后从B冲出,在空中能上升的最大高度为![]() (不计空气阻力),则( )
(不计空气阻力),则( )
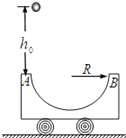
A. 小球和小车组成的系统动量守恒
B. 小车向左运动的最大距离为![]()
C. 小球离开小车后做斜上抛运动
D. 小球第二次能上升的最大高度![]()
【答案】D
【解析】
试题小球与小车组成的系统在水平方向所受合外力为零,水平方向系统动量守恒,但系统整体所受合外力不为零,系统动量不守恒,故A错误;系统水平方向动量守恒,以向右为正方向,在水平方向,由动量守恒定律得:mv-mv′=0,![]() ,解得,小车的位移:x=R,故B错误;小球与小车组成的系统在水平方向动量守恒,小球由A点离开小车时系统水平方向动量为零,小球与小车水平方向速度为零,小球离开小车后做竖直上抛运动,故C错误;小球第一次车中运动过程中,由动能定理得:mg(h0-
,解得,小车的位移:x=R,故B错误;小球与小车组成的系统在水平方向动量守恒,小球由A点离开小车时系统水平方向动量为零,小球与小车水平方向速度为零,小球离开小车后做竖直上抛运动,故C错误;小球第一次车中运动过程中,由动能定理得:mg(h0-![]() h0)-Wf=0,Wf为小球克服摩擦力做功大小,解得:Wf=
h0)-Wf=0,Wf为小球克服摩擦力做功大小,解得:Wf=![]() mgh0,即小球第一次在车中滚动损失的机械能为
mgh0,即小球第一次在车中滚动损失的机械能为![]() mgh0,由于小球第二次在车中滚动时,对应位置处速度变小,因此小车给小球的弹力变小,摩擦力变小,摩擦力做功小于
mgh0,由于小球第二次在车中滚动时,对应位置处速度变小,因此小车给小球的弹力变小,摩擦力变小,摩擦力做功小于![]() mgh0,机械能损失小于
mgh0,机械能损失小于![]() mgh0,因此小球再次离开小车时,能上升的高度大于:
mgh0,因此小球再次离开小车时,能上升的高度大于:![]() h0-
h0-![]() h0=
h0=![]() h0,而小于
h0,而小于![]() h0,故D正确;故选D。
h0,故D正确;故选D。

 阅读快车系列答案
阅读快车系列答案【题目】在验证牛顿第二定律实验中,小车及车中砝码的质量用M表示,桶及桶中砝码的质量用m表示,小车的加速度可由小车后拖动的纸带通过打点计时器打出的点计算出。

(1)某组同学用如图甲所示装置,采用控制变量的方法,来研究M不变的情况下,小车的加速度a与小车受到的力的关系。下列操作不正确的是______。
![]() 首先要平衡摩擦力,使小车受到的合力就是细绳对小车的拉力
首先要平衡摩擦力,使小车受到的合力就是细绳对小车的拉力
![]() 平衡摩擦力的方法就是,在塑料小桶中添加砝码,使小车能匀速滑动
平衡摩擦力的方法就是,在塑料小桶中添加砝码,使小车能匀速滑动
![]() 每次改变拉小车的拉力后都需要重新平衡摩擦力
每次改变拉小车的拉力后都需要重新平衡摩擦力
![]() 实验中通过在塑料桶中增加砝码来改变小车受到的拉力
实验中通过在塑料桶中增加砝码来改变小车受到的拉力
![]() 实验中将小车靠近打点计时器,然后先放小车,再开打点计时器的开关
实验中将小车靠近打点计时器,然后先放小车,再开打点计时器的开关
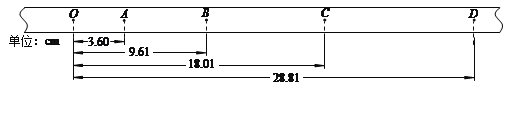
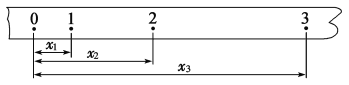
(2)该同学得到如图乙所示的纸带,A、B、C、D、E、F、G是纸带上7个连续的点。相邻两点间的时间![]() 由此可算出小车的加速度
由此可算出小车的加速度![]() ______。
______。
(3)该同学测得小车质量M一定时,a与F的数据资料如下表所示。根据表中数据,在右图坐标系中描点画出图丙![]() 图象________:根据图象可以得出结论:______。
图象________:根据图象可以得出结论:______。
|
|
|
|
|
|
|
|
|
|
(4)某组同学实验得出数据,画出![]() 图象如图丁所示,那么该组同学实验中出现的问题可能是______。
图象如图丁所示,那么该组同学实验中出现的问题可能是______。
A.实验中摩擦力没有平衡或平衡不足
B.实验中摩擦力平衡过度
C.实验中小车及其上砝码质量太大
D.实验中小车质量发生变化
(5)在验证加速度与质量的实验中,保持桶及桶中砝码的质量m一定,改变小车及车中砝码的总质量M测出相应的加速度,采用图象法处理数据。为了比较容易地确定出加速度a与质量M的关系,应该作a与______的图象。
(6)若实验过程中不满足![]() 的条件,结果得到的图象可能是下图中______。
的条件,结果得到的图象可能是下图中______。
A. 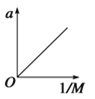 B.
B. 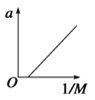 C.
C.  D.
D.