题目内容
6.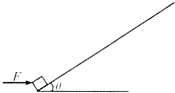 如图,质量为lkg的小物体在大小为30N的水平恒力F作用下,从倾角θ=37°的足够长斜面底端由静止开始运动,物体与斜面间的动摩擦因数为0.5,2s后撤去F.求此后再经过多长时间物体回到斜面底端.(取g=10m/s2,sin37°=0.6,cos37°=0.8)
如图,质量为lkg的小物体在大小为30N的水平恒力F作用下,从倾角θ=37°的足够长斜面底端由静止开始运动,物体与斜面间的动摩擦因数为0.5,2s后撤去F.求此后再经过多长时间物体回到斜面底端.(取g=10m/s2,sin37°=0.6,cos37°=0.8)
分析 根据牛顿第二定律求出物体在水平拉力作用下的加速度,结合速度时间公式求出求出2s后的速度,通过位移时间公式求出2s内的位移,再根据牛顿第二定律求出撤去拉力后的加速度,结合速度位移公式求出匀减速运动的位移,从而得出物体向上运动的最高点的位置.撤去拉力后求出速度减为零的时间,根据牛顿第二定律求出返回时的加速度,结合位移时间公式求出返回的时间,从而得出总时间.
解答  解:(1)根据牛顿第二定律得,匀加速上滑的加速度为:
解:(1)根据牛顿第二定律得,匀加速上滑的加速度为:
${a}_{1}=\frac{Fcos37°-μ(mgcos37°+Fsin37°)-mgsin37°}{m}$
代入数据解得:${a}_{1}=5m/{s}^{2}$,
则2s末的速度为:v1=a1t1=5×2m/s=10m/s,
2s内的位移为:${x}_{1}=\frac{{v}_{1}^{2}}{2{a}_{1}}$=$\frac{1{0}^{2}}{2×5}=10$m,
撤去拉力后的加速度为:${a}_{2}=\frac{mgsin37°+μmgcos37}{m}$=gsin37°+μgcos37°=6+0.5×8m/s2=10m/s2.
则匀减速运动的位移大小为:${x}_{2}=\frac{{v}_{1}^{2}}{2{a}_{2}}$=$\frac{1{0}^{2}}{2×10}$=5m,
则物体向上运动的最高点的位置为:x=x1+x2=10+5m=15m.
物体匀减速运动的到最高点的时间为:${t}_{2}=\frac{{v}_{1}}{{a}_{2}}$=$\frac{10}{10}s=1$s,
物体返回做匀加速运动的加速度为:${a}_{3}=\frac{mgsin37°-μmgcos37°}{m}$=gsin37°-μgcos37°=6-0.5×8=2m/s2,
根据x=$\frac{1}{2}{a}_{3}{t}_{3}^{2}$得:${t}_{3}=\sqrt{\frac{2x}{{a}_{3}}}=\sqrt{\frac{2×15}{2}}s=\sqrt{15}s≈3.87$s.
则:t=t2+t3=1+3.87s=4.87s.
答:此后再经过4.87s的时间物体回到斜面底端
点评 解决本题的关键理清物体的运动规律,结合牛顿第二定律和运动学公式综合求解,知道加速度是联系力学和运动学的桥梁.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案| A. | 轨迹为圆 | B. | 轨迹为抛物线 | ||
| C. | 加速度的大小和方向均不变 | D. | 速度的大小和方向均不变 |
| A. | 物体加速度表示增加的速度 | |
| B. | 物体速度变化量越大,则加速度越大 | |
| C. | 物体速度变化越快,则速度的变化率越大,加速度也越大 | |
| D. | 加速度很大时,运动物体的速度一定很快变大 |
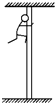 如图所示,一名消防队员在模拟演习训练中,沿着长为12m的竖立在地面上的钢管向下滑.他从钢管顶端由静止开始先匀加速再匀减速下滑,滑到地面时速度恰好为零.如果他加速时的加速度大小是减速时的2倍,下滑的总时间为3s,那么该消防队员( )
如图所示,一名消防队员在模拟演习训练中,沿着长为12m的竖立在地面上的钢管向下滑.他从钢管顶端由静止开始先匀加速再匀减速下滑,滑到地面时速度恰好为零.如果他加速时的加速度大小是减速时的2倍,下滑的总时间为3s,那么该消防队员( )| A. | 下滑过程中的最大速度为4m/s | |
| B. | 加速与减速过程的时间之比为1:2 | |
| C. | 加速与减速过程中平均速度之比为1:2 | |
| D. | 减速过程的加速度大小为4m/s2 |
 如图所示,粗糙水平圆盘上,质量相等的A、B两物块叠放在一起,随圆盘一起做匀速圆周运动,则下列说法正确的是( )
如图所示,粗糙水平圆盘上,质量相等的A、B两物块叠放在一起,随圆盘一起做匀速圆周运动,则下列说法正确的是( )| A. | B的向心力是A的向心力的2倍 | |
| B. | 盘对B的摩擦力与B对A的摩擦力相等 | |
| C. | A、B都有沿半径向外滑动的趋势 | |
| D. | 若B先滑动,则B对A的动摩擦因数μA小于盘对B的动摩擦因数μB |
| A. | 匀速直线运动 | B. | 平抛运动 | C. | 匀加速直线运动 | D. | 变速曲线运动 |
| A. | 只有体积小到可以忽略的带电体才能看成点电荷 | |
| B. | 丝绸摩擦过的玻璃棒带正电 | |
| C. | 将分别带有等量正电和负电的物体相互接触,电荷发生中和消失了 | |
| D. | 带电体的电荷量可能为2.4×10-19C |
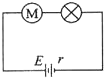 如图所示,电源电动势为E=30V,内阻不计,电灯上标有“6V 12W”字样,直流电动机线圈电阻R=2Ω,若电灯恰能正常发光,求电动机输出的机械功率.
如图所示,电源电动势为E=30V,内阻不计,电灯上标有“6V 12W”字样,直流电动机线圈电阻R=2Ω,若电灯恰能正常发光,求电动机输出的机械功率. 如图所示,在光滑的水平地面上静止着质量为m的木块,一粒质量为m初速为v0的子弹水平击中木块,并留在木块中,求:
如图所示,在光滑的水平地面上静止着质量为m的木块,一粒质量为m初速为v0的子弹水平击中木块,并留在木块中,求: