题目内容
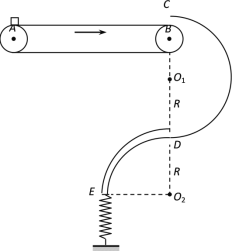
【题目】如图所示,水平传送带顺时针匀速传动,紧靠传送带右端B的竖直平面内固定有一个光滑半圆轨道CD,半圆轨道下端连接有内壁光滑的![]() 细圆管DE,一劲度系数k=100 N/m的轻弹簧一端固定在地面,自由伸长时另一端刚好在管口E处。质量m=1 kg的小物块轻放在传送带的左端A点,随后经B、 C间的缝隙进入CD,并恰能沿CD做圆周运动。小物块经过D点后进入DE,随后压缩弹簧,速度最大时弹簧的弹性势能EP=0.5 J。已知CD和DE的半径均为R=0.9 m,取g=10 m/s2,求:
细圆管DE,一劲度系数k=100 N/m的轻弹簧一端固定在地面,自由伸长时另一端刚好在管口E处。质量m=1 kg的小物块轻放在传送带的左端A点,随后经B、 C间的缝隙进入CD,并恰能沿CD做圆周运动。小物块经过D点后进入DE,随后压缩弹簧,速度最大时弹簧的弹性势能EP=0.5 J。已知CD和DE的半径均为R=0.9 m,取g=10 m/s2,求:
(1)传送带对小物块做的功W;
(2)小物块刚到达D点时轨道CD对小物块的支持力大小ND;
(3)小物块的最大速度vm。
【答案】(1)4.5 J (2)60 N (3)8 m/s
【解析】
(1)由于小物块恰能沿CD做圆周运动,设在C点时的速度为vC,则有mg = m![]() ,根据动能定理得W =
,根据动能定理得W =![]() mvC2 解得W = 4.5 J
mvC2 解得W = 4.5 J
(2)由C点到D点,根据机械能守恒定律有 2mgR =![]() mvD2-
mvD2-![]() mvC2 ND-mg = m
mvC2 ND-mg = m![]() 解得 ND = 60 N
解得 ND = 60 N
(3)当弹簧弹力等于小物块重力时,小物块速度最大,设此时弹簧压缩量为x,则有kx = mg ,小物块从D点到速度最大时,根据能量守恒定律有mg(R+x) =![]() mvm2-
mvm2-![]() mvD2 + EP
mvD2 + EP
解得 vm = 8 m/s

练习册系列答案
相关题目