题目内容
如图所示，一平直的传送带以速度v=2m/s匀速运动，传送带把A处的工件运送到B处，A、B相距L=10m。从A处把工件无初速地放到传送带上，经过时间t=6s能传送到B处。欲用最短的时间把工件从A 处传送到B处，求传送带的运行速度至少多大。
解：因为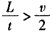
，所以工件在6s内先匀加速运动，后匀速运动，有
x1=vt1/2，x2=vt2，t1+t2=t，x1+x2=L
解上述四式得t1=2 s，则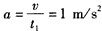
若要把工件以最短时间传送到B，则应使工件始终加速直至B处，工件加速度仍为a，设传送带最小速度为v'
，v'=at'
解得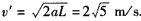
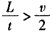，所以工件在6s内先匀加速运动，后匀速运动，有x1=vt1/2，x2=vt2，t1+t2=t，x1+x2=L
解上述四式得t1=2 s，则
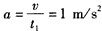
若要把工件以最短时间传送到B，则应使工件始终加速直至B处，工件加速度仍为a，设传送带最小速度为v'
，v'=at' 解得
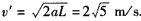
练习册系列答案
相关题目
如图所示，一平直的传送带以速率v=2m/s匀速运动，传送带与水平面夹角为θ=30°，传送带把A处的工件不断地运到较高的B处，A、B两处相距L=30m．从A处把工件轻轻地放到传送带上，经过时间t=20s能传到B处．假设A处每隔一定时间放上一工件，每小时恰好运送7200个工件，每个工件的质量为m=2kg，求：（g=10m/s2）
