题目内容

如图所示半径为R、r(R>r)甲、乙两圆形轨道安置在同一竖直平面内,两轨道之间由一条水平轨道(CD)相连,如小球从离地3R的高处A点由静止释放,可以滑过甲轨道,经过CD段又滑上乙轨道后离开两圆形轨道,小球与CD段间的动摩擦因数为μ,其余各段均光滑.为避免出现小球脱离圆形轨道而发生撞轨现象.试设计CD段的长度.
CD≤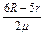 或
或 ≤CD <
≤CD <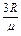
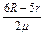 或
或 ≤CD <
≤CD <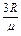
小球在甲轨道上做圆周运动通过最高点的最小速度为

设小球能通过甲轨道最高点时速度为v1.
由机械能守恒定律得:
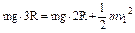

∵
 >
> ∴小球能通过甲轨道而不撞轨
∴小球能通过甲轨道而不撞轨设CD的长度为x,小球在乙轨道最高点的最小速度为

小球要通过乙轨道最高点,则需满足:
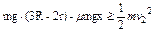 得:
得:x≤
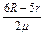
小球到乙轨圆心等高处之前再返回,则需满足:
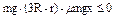 且
且 得:
得: ≤x <
≤x <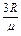
总结论:CD≤
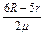 或
或 ≤CD <
≤CD <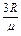

练习册系列答案
相关题目

 此时弹簧恰好为自然长度。现使挡板以恒定加速度a=2m/s2匀加速沿斜面向下运动(斜面足够长),己知弹簧的劲度系数k=50N/m。求:
此时弹簧恰好为自然长度。现使挡板以恒定加速度a=2m/s2匀加速沿斜面向下运动(斜面足够长),己知弹簧的劲度系数k=50N/m。求:


 ;
;
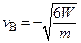 (“-”表示B的速度方向与A的速度方向相反)
(“-”表示B的速度方向与A的速度方向相反)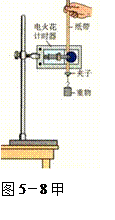
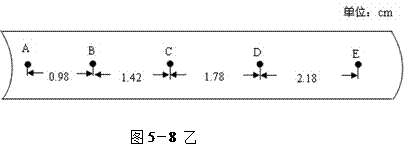


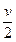 的速度向右运动
的速度向右运动
