题目内容
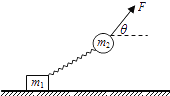
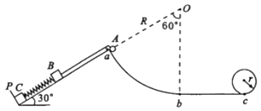
【题目】如图所示，倾角30°的光滑斜面上，劲度系数k=5N/m的轻质弹簧两端连接着两个质量均为m=1kg的物块B和C，C紧靠着挡板P，B通过轻质细绳跨过光滑定滑轮与质量M=8kg的物块A连接，细绳平行于斜面，A在外力作用下静止在圆心角为60°的六分之一光滑圆弧轨道的顶端a处，此时绳子恰好拉直且无张力；圆弧轨道最低端b与光滑水平轨道相切。现由静止释放A，当A滑至圆弧轨道最低点b时，C恰好离开挡板P（B未到达斜面最高点），此时绳子突然断裂。重力加速度取
，弹簧的形变始终在弹性限度内，细绳不可伸长：（已知
）
(1)求从一开始到绳子断裂物块B的位移的大小；
(2)求当物块A滑至b处，绳子断后瞬间，A的速度大小。
【答案】(1)2m；(2)
【解析】
(1)A位于a处时，细绳无张力且物块B静止，对B由力的平衡，弹簧压缩
当C恰好离开挡板P时，对C由力的平衡，弹簧拉伸
可得B的位移
=2m
(2)A在a处与在b处时，A、B的系统由机械能守恒
；
A、B沿着绳子方向的速度大小相等
解得
练习册系列答案
相关题目
