题目内容
【题目】两个带电小球A和B,质量分别为![]() 、
、![]() ,带有同种电荷,带电量分别为
,带有同种电荷,带电量分别为![]() 、
、![]() 、B两球均放在光滑绝缘的水平板上,A球固定,B球被质量为
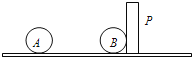
、B两球均放在光滑绝缘的水平板上,A球固定,B球被质量为![]() 的绝缘挡板P挡住静止,A、B两球相距为d,如图所示
的绝缘挡板P挡住静止,A、B两球相距为d,如图所示![]() 某时刻起挡板P在向右的水平力F作用下开始向右做匀加速直线运动,加速度大小为a,经过一段时间带电小球B与挡板P分离,在此过程中力F对挡板做功
某时刻起挡板P在向右的水平力F作用下开始向右做匀加速直线运动,加速度大小为a,经过一段时间带电小球B与挡板P分离,在此过程中力F对挡板做功![]() 求:
求:
![]() 力F的最大值和最小值?
力F的最大值和最小值?
![]() 带电小球B与挡板分离时的速度?
带电小球B与挡板分离时的速度?
![]() 从开始运动到带电小球与挡板P分离的过程中,电场力对带电小球B做的功?
从开始运动到带电小球与挡板P分离的过程中,电场力对带电小球B做的功?
【答案】(1) ![]() ;
; ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】
两种电荷间存在斥力,在斥力作用下,B球先与P板一起向右做匀加速运直到两者分离,库仑斥力不断减小,以B和P整体为研究对象,可知,开始运动时力F最小,分离时力F最大,根据牛顿第二定律和库仑定律求解;![]() 球与挡板分离时,以B球为研究对象,由牛顿第二定律求出加速度,再运用运动学公式求解B、P分离时的速度;对挡板应用动能定理求出电场力对带电小球B做的功;
球与挡板分离时,以B球为研究对象,由牛顿第二定律求出加速度,再运用运动学公式求解B、P分离时的速度;对挡板应用动能定理求出电场力对带电小球B做的功;
解:![]() 开始运动时力F最小,以B球和挡板为研究对象,由牛顿第二定律
开始运动时力F最小,以B球和挡板为研究对象,由牛顿第二定律![]()
解得最小力为:![]()
B球与挡板分离后力F最大,以挡板为研究对象,由牛顿第二定律解得最大力为:![]()
![]() 球与挡板分离时,以B球为研究对象,由牛顿第二定律得:
球与挡板分离时,以B球为研究对象,由牛顿第二定律得:![]()
B球匀加速直线运动的位移为:![]()
又由运动学公式得:![]()
联立解得带电小球B与挡板分离时的速度为: ![]()
![]() 设B球对挡板做功
设B球对挡板做功![]() ,挡板对B球做功
,挡板对B球做功![]() ,电场力对B球做功
,电场力对B球做功![]() ,在B球与挡板共同运动的过程中,对挡板应用动能定理得:
,在B球与挡板共同运动的过程中,对挡板应用动能定理得:![]()
挡板对B球做的功![]()
对B球应用动能定理得:![]()
联立解得电场力对B球做功为:![]()

练习册系列答案
相关题目