题目内容
质量均为1kg的小滑块(可视为质点A、B,与水平面间的动摩擦因数均为μ=0.1.当A、B间的距离5m<L≤10m时,其间存在大小为2N的恒定引力;当L<5m时,其间存在大小为2N的恒定斥力.今让A以某一初速度向着静止的B运动,当与B间的距离为10m时,A的速度为v=4m/s.g取10m/s2
求:
(1)A、B间的距离从L1=10m减小到L2=5m过程中经历的时间.
(2)A、B能靠近到的最小距离.
【答案】分析:(1)根据牛顿第二定律求出加速度的大小,结合位移关系,运用运动学发生求出A、B间的距离从L1=10m减小到L2=5m过程中经历的时间.
(2)根据速度时间公式求出相距5m时A、B的速度,通过牛顿第二定律求出A、B之间为斥力时的加速度.B速度减为零后反向运动,抓住A、B速度相同时,距离最短,结合运动学公式求出A、B能靠近到的最小距离.
解答:解:(1)在L从L1变到L2的过程中,A、B均做匀加速运动,且加速度大小相同.
有:F-μmg=ma1


xA+xB=L1-L2
代入数据解得t1=1s.
(2)t1时刻,A、B的速度大小分别为
v1A=v+a1t1
v1B=a1t1
(v1A=5m/s,v1B=1m/s)
之后,A、B均做匀减速运动且加速度大小相等.
F+μmg=ma2
解得
B的速度减小到零经历的时间 为t2.
则0-v1B=-at2
解得 .
.
然后B反向加速,加速度大小a3=a1
当B与A速度相同时,二者距离最小,设此时的速度为v.
对B:v=a3t3
对A:v=v1A-a2(t2+t3)
解得t3=1s,v=1m/s
在t2、t3时间内,A、B的位移分别为:


解得xA′=4m,
由几何关系知xA′+△x=L2+xB′
代入数据解得 .
.
答:(1)A、B间的距离从L1=10m减小到L2=5m过程中经历的时间为1s.
(2)A、B能靠近到的最小距离为 .
.
点评:解决本题的关键理清物体的运动过程,结合牛顿第二定律和运动学公式进行分析求解.
(2)根据速度时间公式求出相距5m时A、B的速度,通过牛顿第二定律求出A、B之间为斥力时的加速度.B速度减为零后反向运动,抓住A、B速度相同时,距离最短,结合运动学公式求出A、B能靠近到的最小距离.
解答:解:(1)在L从L1变到L2的过程中,A、B均做匀加速运动,且加速度大小相同.
有:F-μmg=ma1


xA+xB=L1-L2
代入数据解得t1=1s.
(2)t1时刻,A、B的速度大小分别为
v1A=v+a1t1
v1B=a1t1
(v1A=5m/s,v1B=1m/s)
之后,A、B均做匀减速运动且加速度大小相等.
F+μmg=ma2
解得

B的速度减小到零经历的时间 为t2.
则0-v1B=-at2
解得
 .
.然后B反向加速,加速度大小a3=a1
当B与A速度相同时,二者距离最小,设此时的速度为v.
对B:v=a3t3
对A:v=v1A-a2(t2+t3)
解得t3=1s,v=1m/s
在t2、t3时间内,A、B的位移分别为:


解得xA′=4m,

由几何关系知xA′+△x=L2+xB′
代入数据解得
 .
.答:(1)A、B间的距离从L1=10m减小到L2=5m过程中经历的时间为1s.
(2)A、B能靠近到的最小距离为
 .
.点评:解决本题的关键理清物体的运动过程,结合牛顿第二定律和运动学公式进行分析求解.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 (2012?东城区一模)如图所示,半径R=0.1m的竖直半圆形光滑轨道bc与水平面ab相切.质量m=0.1kg的小滑块B放在半圆形轨道末端的b点,另一质量也为m=0.1kg的小滑块A以v0=2
(2012?东城区一模)如图所示,半径R=0.1m的竖直半圆形光滑轨道bc与水平面ab相切.质量m=0.1kg的小滑块B放在半圆形轨道末端的b点,另一质量也为m=0.1kg的小滑块A以v0=2
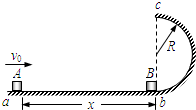 如图所示,半径R=0.1m的竖直半圆形光滑轨道bc与水平面ab相切.质量m=0.1kg的小滑块B放在半圆形轨道末端的b点,另一质量也为m=0.1kg的小滑块A,以v0=2
如图所示,半径R=0.1m的竖直半圆形光滑轨道bc与水平面ab相切.质量m=0.1kg的小滑块B放在半圆形轨道末端的b点,另一质量也为m=0.1kg的小滑块A,以v0=2