题目内容
半径为R的半圆形光滑轨道竖直固定在水平地面上，A点是最低点，B点是最高点，如图所示，质量为M的小球以某一速度自A点进入轨道，它经过最高点后飞出，最后落在水平地面上的C点，现测得AC=2R，求小球自A点进入轨道时的速度大小？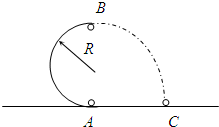
小球从B到C过程为平抛运动，根据平抛运动的分位移公式，有
水平方向：2R=vBt ①
竖直方向：2R=
gt2 ②
小球从A到B过程只有重力做功，机械能守恒，根据守恒定律，有
Mg（2R）=
M
-
M
③
联立①②②解得
vB=
答：小球自A点进入轨道时的速度大小为
．
水平方向：2R=vBt ①
竖直方向：2R=
| 1 |
| 2 |
小球从A到B过程只有重力做功，机械能守恒，根据守恒定律，有
Mg（2R）=
| 1 |
| 2 |
| v | 2A |
| 1 |
| 2 |
| v | 2B |
联立①②②解得
vB=
| 5gR |
答：小球自A点进入轨道时的速度大小为
| 5gR |
练习册系列答案
相关题目
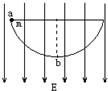如图所示，质量为m，带电量+q的小球置于半径为R的半圆形光滑轨道内，整个装置处于场强为E的竖直向下匀强电场中，小球从水平直径位置上的a点由静止释放，则小球经过最低点b时轨道对小球支持力的大小为
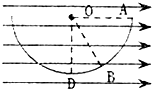有一半径为R的半圆形光滑绝缘槽，置于水平向右的匀强电场中，若把一个带正电且电荷量为q、质量为m的小球放置在槽的B点时刚好静止，已知OB与竖直方向成37°角．若使小球从槽的边缘A点由静止滑下，求：（其中sin37°=0.6，cos37°=0.8）
如图所示，一半径为R的半圆形光滑轨道放在水平面上，A为轨道与水平面的切点，A左边的水平面是光滑的，半圆形光滑轨道固定．一个质量为m的小球以某一速度冲上轨道，小球落地点为C．当小球将要从轨道口飞出时，轨道的压力恰好为零．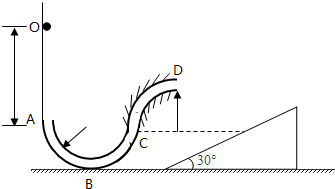
如图所示，竖直光滑直轨道OA高度为2R，连接半径为R的半圆形光滑环形管道ABC（B为最低点），其后连接
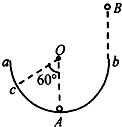如图所示，一半径为R的半圆形光滑轨道固定在竖直平面内．a、b是轨道的两端点且高度相同，O为圆心．小球A静止在轨道的最低点，小球B从轨道右端b点的正上方距b点高为2R处由静止自由落下，从b点沿圆弧切线进入轨道后，与小球A相碰．第一次碰撞后B球恰返回到b点，A球上升的最高点为c，Oc连线与竖直方向夹角为60°（两球均可视为质点）．求A、B两球的质量之比mA：mB．（结果可以用根式表示）