题目内容
2.在x轴上有两个点电荷,A带正电+Q,B带负电-2Q,在x轴上相距为L,场强大小相等的点有几处?每处合场强大小分别为多少?分析 根据点电荷的电场强度公式E=k$\frac{Q}{{r}^{2}}$,结合题意可确定电场强度大小相等的位置.并由电场的叠加原理求解合场强的大小.
解答 解:设场强大小相等的点到A的距离为x.根据点电荷的电场强度可知:
k$\frac{Q}{{x}^{2}}$=k$\frac{2Q}{(L-x)^{2}}$,则有:
代入数据解得:x=($\sqrt{2}$±1)L
故场强大小相等的点有两处:
一处是两点电荷的连线间,合场强为 E=2k$\frac{Q}{{x}^{2}}$=2k$•\frac{Q}{(\sqrt{2}-1)^{2}{L}^{2}}$=$\frac{2kQ}{(3-2\sqrt{2}){L}^{2}}$
另一处是AB连线上A的外侧,合场强为0.
答:在x轴上相距为L,场强大小相等的点有两处:一处是两点电荷的连线间,合场强为$\frac{2kQ}{(3-2\sqrt{2}){L}^{2}}$.另一处是AB连线上A的外侧,合场强为0.
点评 考查点电荷在某处电场强度的叠加,注意电场强度的大小与方向.同时根据题意两者间距不定,所以只要满足间距的关系,即可找到电场强度大小相等的点.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
12.下列说法正确的是( )
| A. | 温度升高,物体的每一个分子的动能都增大 | |
| B. | 外界对气体做功,气体的内能一定增大 | |
| C. | 当两个分子间的距离为r0(平衡位置)时,分子力为零,分子势能最小 | |
| D. | 布朗运动是悬浮在液体中固体颗粒分子的无规则运动 |
10.使用电压表要注意量程的选择.现有电动势约为4.5V的电源,为了精确测量其电动势,应选用电压表的量程为( )
| A. | 1.5V | B. | 6V | C. | 12V |
7.地球的第一宇宙速度大小为v,在地面上用弹簧测力计测量一质量为m的物体的重力,物体静止时,弹簧测力计的示数为F.已知引力常量为G,忽略地球自转的影响,则地球的质量为( )
| A. | $\frac{{m{v^2}}}{GF}$ | B. | $\frac{{m{v^4}}}{GF}$ | C. | $\frac{{F{v^2}}}{Gm}$ | D. | $\frac{{F{v^4}}}{Gm}$ |
11.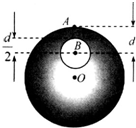 如图所示,O为地球球心,A为地球表面上的点,B为O、A连线间的点,AB=d,将地球视为质量分布均匀的球体,半径为R.设想挖掉以B为圆心、以$\frac{d}{2}$为半径的球.若忽略地球自转,则挖出球体后A点的重力加速度与挖去球体前的重力加速度之比为( )
如图所示,O为地球球心,A为地球表面上的点,B为O、A连线间的点,AB=d,将地球视为质量分布均匀的球体,半径为R.设想挖掉以B为圆心、以$\frac{d}{2}$为半径的球.若忽略地球自转,则挖出球体后A点的重力加速度与挖去球体前的重力加速度之比为( )
 如图所示,O为地球球心,A为地球表面上的点,B为O、A连线间的点,AB=d,将地球视为质量分布均匀的球体,半径为R.设想挖掉以B为圆心、以$\frac{d}{2}$为半径的球.若忽略地球自转,则挖出球体后A点的重力加速度与挖去球体前的重力加速度之比为( )
如图所示,O为地球球心,A为地球表面上的点,B为O、A连线间的点,AB=d,将地球视为质量分布均匀的球体,半径为R.设想挖掉以B为圆心、以$\frac{d}{2}$为半径的球.若忽略地球自转,则挖出球体后A点的重力加速度与挖去球体前的重力加速度之比为( )| A. | 1-$\frac{d}{4R}$ | B. | 1-$\frac{d}{8R}$ | C. | 1-$\frac{d}{R}$ | D. | $\frac{d}{R-d}$ |
12.有两个匀强磁场区域Ⅰ和Ⅱ,I中的磁感应强度是Ⅱ中的k倍,两个速率相同的电子分别在两磁场区域做圆周运动.与Ⅰ中运动的电子相比,Ⅱ中的电子( )
| A. | 运动轨迹的半径是Ⅰ中的k倍 | B. | 加速度的大小是Ⅰ中的k倍 | ||
| C. | 做圆周运动的周期是Ⅰ中的k倍 | D. | 做圆周运动的角速度是Ⅰ中的k倍 |

 如图所示,带斜面的小车在水平地面上,斜面倾角为θ,仅靠斜面有一质量为m的光滑球,试求在下列状态下斜面对小球的弹力大小:
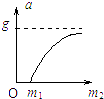
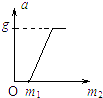
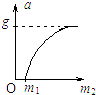
如图所示,带斜面的小车在水平地面上,斜面倾角为θ,仅靠斜面有一质量为m的光滑球,试求在下列状态下斜面对小球的弹力大小: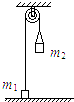 如图所示,轻绳跨过光滑的定滑轮,一端系一质量为m1的物体,另一端系一质量为m2的砂桶.当m2变化时,m1的加速度a的大小与m2的关系图线可能是( )
如图所示,轻绳跨过光滑的定滑轮,一端系一质量为m1的物体,另一端系一质量为m2的砂桶.当m2变化时,m1的加速度a的大小与m2的关系图线可能是( )