题目内容
12.有两个匀强磁场区域Ⅰ和Ⅱ,I中的磁感应强度是Ⅱ中的k倍,两个速率相同的电子分别在两磁场区域做圆周运动.与Ⅰ中运动的电子相比,Ⅱ中的电子( )| A. | 运动轨迹的半径是Ⅰ中的k倍 | B. | 加速度的大小是Ⅰ中的k倍 | ||
| C. | 做圆周运动的周期是Ⅰ中的k倍 | D. | 做圆周运动的角速度是Ⅰ中的k倍 |
分析 电子在磁场中做的圆周运动,洛伦兹力作为向心力,根据圆周运动的周期公式和半径公式逐项分析即可.
解答 解:设Ⅱ中的磁感应强度为B,则Ⅰ中的磁感应强度为kB,
A、根据电子在磁场中运动的半径公式r=$\frac{mv}{qB}$可知,Ⅰ中的电子运动轨迹的半径为$\frac{mv}{qkB}$,Ⅱ中的电子运动轨迹的半径为$\frac{mv}{qB}$,所以Ⅱ中的电子运动轨迹的半径是Ⅰ中的k倍,所以A正确;
B、电子在磁场运动的洛伦兹力作为向心力,所以电子的加速度的大小为a=$\frac{qvB}{m}$,所以Ⅰ中的电子加速度的大小为$\frac{qvkB}{m}$,Ⅱ中的电子加速度的大小为$\frac{qvB}{m}$,所以Ⅱ的电子的加速度大小是Ⅰ中的$\frac{1}{k}$倍,所以B错误;
C、根据电子在磁场中运动的周期公式T=$\frac{2πm}{qB}$可知,Ⅰ中的电子运动周期为$\frac{2πm}{qkB}$,Ⅱ中的电子运动周期为$\frac{2πm}{qB}$,所以Ⅱ中的电子运动轨迹的半径是Ⅰ中的k倍,所以Ⅱ中的电子运动轨迹的周期是Ⅰ中的k倍,所以C正确;
D、做圆周运动的角速度ω=$\frac{2π}{T}=\frac{2π}{\frac{2πm}{qB}}=\frac{qB}{m}$,所以Ⅰ中的电子运动角速度为$\frac{qkB}{m}$,Ⅱ中的电子运动角速度为$\frac{qB}{m}$,在Ⅱ的电子做圆周运动的角速度是Ⅰ中的$\frac{1}{k}$倍,所以D错误;
故选:AC.
点评 本题是对粒子在磁场中做圆周运动的基本考查,解决本题的关键是抓住洛伦兹力作为向心力,根据向心力的不同的公式来分析不同的关系,记住平时的得出的结论可以快速的分析问题.

 阅读快车系列答案
阅读快车系列答案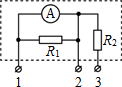 如图所示,其中电流表A的量程为0.6A,表盘均匀划分为30个小格,每一小格表示0.02A,R1的阻值等于电流表内阻的$\frac{1}{2}$; R2的阻值等于电流表内阻的2倍.若用电流表A的表盘刻度表示流过接线柱1的电流值,则下列分析正确的是( )
如图所示,其中电流表A的量程为0.6A,表盘均匀划分为30个小格,每一小格表示0.02A,R1的阻值等于电流表内阻的$\frac{1}{2}$; R2的阻值等于电流表内阻的2倍.若用电流表A的表盘刻度表示流过接线柱1的电流值,则下列分析正确的是( )| A. | 将接线柱 1、2 接入电路时,每一小格表示0.04A | |
| B. | 将接线柱 1、2 接入电路时,每一小格表示0.02A | |
| C. | 将接线柱 1、3 接入电路时,每一小格表示0.06A | |
| D. | 将接线柱 1、3 接入电路时,每一小格表示0.01A |
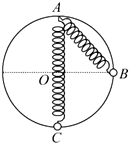 如图所示,质量为m的小球穿在半径为R的光滑圆环上,可以沿圆环自由滑动,连接小球的轻质弹簧另一端固定在圆环的最高点.现将小球从圆环的水平直径右端B点静止释放,此时弹簧处于自然长度.当小球运动至圆环最低点C时速度为v,此时小球与圆环之间没有弹力.运动过程中弹簧始终处在弹性限度内,则下面判断正确的是( )
如图所示,质量为m的小球穿在半径为R的光滑圆环上,可以沿圆环自由滑动,连接小球的轻质弹簧另一端固定在圆环的最高点.现将小球从圆环的水平直径右端B点静止释放,此时弹簧处于自然长度.当小球运动至圆环最低点C时速度为v,此时小球与圆环之间没有弹力.运动过程中弹簧始终处在弹性限度内,则下面判断正确的是( )| A. | 小球在B点的加速度小于g,方向竖直向下 | |
| B. | 该过程中小球的机械能守恒 | |
| C. | 在C点弹簧的弹性势能等于mgR-$\frac{1}{2}$mv2 | |
| D. | 该过程中小球重力做的功等于其动能的增量 |
 如图所示,实线是一簇未标明方向的由点电荷产生的电场线,虚线是某一带电粒子通过该电场区域时的运动轨迹,a、b是轨迹上的两点.带电粒子在运动中只受电场力作用,根据此图可作出正确判断的是( )
如图所示,实线是一簇未标明方向的由点电荷产生的电场线,虚线是某一带电粒子通过该电场区域时的运动轨迹,a、b是轨迹上的两点.带电粒子在运动中只受电场力作用,根据此图可作出正确判断的是( )| A. | 该粒子带负电 | B. | b点的电势高于a点的电势 | ||
| C. | 粒子在a、b两点的速度a处较大 | D. | 粒子在a、b两点的加速度b处较小 |
 为了测定一节新干电池的电动势和内阻(约为0.3Ω),配备的器材有:
为了测定一节新干电池的电动势和内阻(约为0.3Ω),配备的器材有: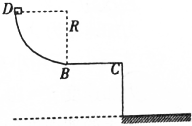 如图所示,半径R=0.8m的四分之一圆弧光滑轨道竖直放置,一长L=1m的水平桌面BC与圆弧轨道的最低点相切于B点,BC离地面高h=0.6m,质量m=1.0kg的小滑块从圆弧顶点D由静止释放,已知滑块与水平桌面间的动摩擦因数μ=0.6,取g=10m/s2.求小滑块落地时的速度大小v.
如图所示,半径R=0.8m的四分之一圆弧光滑轨道竖直放置,一长L=1m的水平桌面BC与圆弧轨道的最低点相切于B点,BC离地面高h=0.6m,质量m=1.0kg的小滑块从圆弧顶点D由静止释放,已知滑块与水平桌面间的动摩擦因数μ=0.6,取g=10m/s2.求小滑块落地时的速度大小v. 如图所示,光滑的水平面连接一个竖直平面内的半圆形光滑轨道,其半径为0.5m,小物体A(质量为m)以速度v0=15m/s与物体B(质量为M)发生正碰后,物体A以v1=5m/s的速度沿原路返回,求:
如图所示,光滑的水平面连接一个竖直平面内的半圆形光滑轨道,其半径为0.5m,小物体A(质量为m)以速度v0=15m/s与物体B(质量为M)发生正碰后,物体A以v1=5m/s的速度沿原路返回,求: 如图,一质量为m、电荷量为q(q>0)的粒子在匀强电场中运动,A、B为其运动轨迹上的两点.已知该粒子在A点的速度大小为v0,方向与电场方向的夹角为60°;它运动到B点时速度方向与电场方向的夹角为30°.不计重力.求A、B两点间的电势差.
如图,一质量为m、电荷量为q(q>0)的粒子在匀强电场中运动,A、B为其运动轨迹上的两点.已知该粒子在A点的速度大小为v0,方向与电场方向的夹角为60°;它运动到B点时速度方向与电场方向的夹角为30°.不计重力.求A、B两点间的电势差.