题目内容
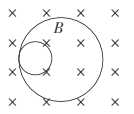
【题目】如图所示，在一竖直放置的圆环形管道内封闭有一定质量的理想气体．用一绝热的固定活塞C和绝热、不计质量、可自由移动的活塞A将管道内气体分隔成体积相等的两部分，A、C与圆环的圆心O等高，两部分气体的温度均为T0=300K．现保持下部分气体的温度不变，对上部分气体缓慢加热至T=500K，求此时活塞A的位置与O点的连线跟竖直方向OB之间的夹角θ．（不计两活塞的体积）
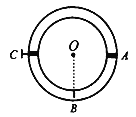
【答案】45°
【解析】
设圆环管道内上下两部分气体的初始体积为V0，加热前后两部分气体的压强分别为P0、P，
上部分气体体积的增加量为△V，对上部分气体，根据理想气体状态方程有
对下部分气体，根据玻意耳定律有
P0V0=P（V0-△V）
解得
△V=
V0
故活塞A的位置与O点的连线和竖直方向的夹角为
θ=45°
练习册系列答案
相关题目
【题目】在“探究弹力和弹簧伸长量的关系，并测定弹簧的劲度系数”实验中，实验装置如图甲所示。实验时先测出不挂钩码时弹簧的自然长度，再将5个钩码逐个挂在绳子的下端，每次测出相应的弹簧总长度。数据记录如下表所示：（弹力始终未超过弹性限度，取
）
记录数据组 | 1 | 2 | 3 | 4 | 5 | 6 |
钩码总质量 | 0 | 30 | 60 | 90 | 120 | 150 |
弹簧总长 | 6.00 | 7.11 | 8.20 | 9.31 | 10.40 | 11.52 |
（1）在图乙坐标系中作出弹簧弹力大小
与弹簧总长度
之间的函数关系的图线_______。
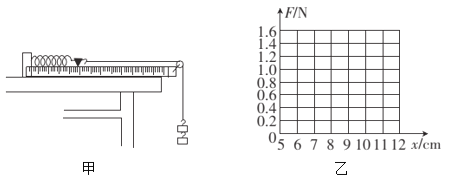
（2）由图线求得该弹簧的劲度系数
__________
。（保留两位有效数字）
