题目内容
在一个圆柱形的、竖直的井里存有一定量的水，井的侧面和底面都是密闭的，在井中固定地插着一根两端开口的薄壁圆管，管和井共轴，管下端未触及井底。在圆柱内有一不漏气的活塞，它可沿圆管上下滑动。开始时，管内外水面相齐，且活塞恰好接触水面，如图5—90所示，现有卷扬机通过绳子对活塞施加一个向上的力F，使活塞缓慢向上移动。已知管筒半径r=0.100m，井的半径R=2r，水的密度ρ=1.00×103kg/m3，大气压p0=1.00×105Pa，求活塞上升H=9.00m的过程中拉力F所做的功。（井和管在水面以上及水面以下的部分都足够长，不计活塞质量，不计摩擦，重力加速度g取10m/s2）
1.65×104J
解析:
题中未明确F是恒力还是变力，故首先要判断清楚。若活塞和水面之间出现真空，则F是恒力。
从开始提升到活塞升至内外水面高度差为
m=10m
的过程中，活塞始终与管内的水接触。设活塞上升距离为h1，管外水面下降距离为h2，则
h0=h1+h2，
因水的体积不变，有 
，
由以上两式得 
m=7.5m。
题给H=9m＞h1，由此可知确实有活塞下面是真空的一段过程。活塞移动距离从0到h1的过程中，对于水和活塞这个整体，其机械能的增加量应等于除重力外其他力所做的功。因为始终无动能，所以机械能的增加量也就等于重力势能的增加量，即
。
其他力有管内、外的大气压力和拉力F，因为水不可压缩，所以管内、外大气压力做的总功为 p0π(R2－r2)h2－p0πr2 h1=0，
故外力做的功就只是拉力F做的功，由功能关系知
W1=
J≈1.18×104J。
活塞移动距离从h到H的过程中，水面不变，F是恒力，
F=πr2p0，
拉力F做功
W2=F(H－h)= πr2p0(H－h1) = π×0.1002×1.0×105×(9.00－7.5)J≈4.71×103J。
所以，拉力F所做的总功为
W=W1+W2=1.18×104J+4.71×103J≈1.65×104J。
（2001?江西）一个圆柱形的竖直的井里存有一定量的水，井的侧面和底部是密闭的，在井中固定地插着一根两端开口的薄壁圆管，管和井共轴，管下端未触及井底．在圆管内有一不漏气的活塞，它可沿圆管上下滑动．开始时，管内外水面相齐，且活塞恰好接触水面，如图所示．现用卷扬机通过绳子对活塞施加一个向上的力F，使活塞缓慢向上移动，已知管筒半径r=0.100m，井的半径R=2r，水的密度ρ=1.00×103kg/m3，大气压ρ0=1.00×105Pa．求活塞上升H=9.00m的过程中拉力F所做的功．（井和管在水面以上及水面以下的部分都足够长．不计活塞质量，不计摩擦，重力加速度g=10m/s2．）
如图1所示，在长约1m的一端封闭的玻璃管中注满清水，水中放一个圆柱形的红蜡块R（圆柱体的直径略小于玻璃管的内径，轻重适宜，使它能在玻璃管内的水中匀速上升），将玻璃管的开口端用胶塞塞紧．将此玻璃管迅速竖直倒置（如图2所示），红蜡块R就沿玻璃管由管口A匀速上升到管底B．若在将玻璃管竖直倒置、红蜡块刚从A端开始匀速上升的同时，将玻璃管由静止开始水平向右匀加速移动（如图3所示），直至红蜡块上升到管底B的位置（如图4所示）．红蜡块与玻璃管间的摩擦很小，可以忽略不计，在这一过程中相对于地面而言（ ）
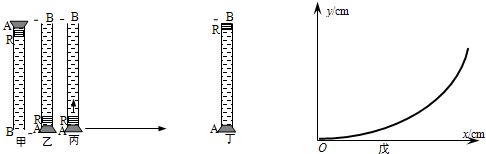
| A、红蜡块沿玻璃管向上做匀速运动，玻璃管向右做匀速运动 | B、红蜡块沿玻璃管向上做匀加速运动，玻璃管向右做匀速运动 | C、红蜡块沿玻璃管向上做匀加速运动，玻璃管向右做匀加速运动 | D、红蜡块沿玻璃管向上做匀速运动，玻璃管向右做匀加速运动 |
