题目内容
在“探究单摆的周期和摆长的关系”实验中.

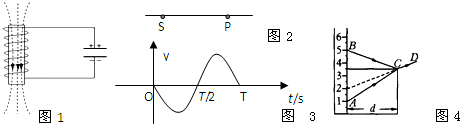
(1)用毫米尺量出悬线的长度L0=97.57cm,用游标卡尺测得摆球直径如图甲所示为d=
(2)根据记录的数据,在坐标纸上以T为纵轴,l为横轴,作出T-l图象,发现图线是曲线;然后尝试以T2为纵轴,l为横轴,作出T2-l图象,发现图线是一条过原点的倾斜直线,由此得出单摆做简谐运动的周期和摆长的关系是
A、T∝
B、T2∝
C、T∝l D、T2∝l
(3)与重力加速度的真实值比较,发现测量结果偏小,分析原因可能是
A、振幅偏小 B、在单摆未悬挂之前先测定其摆长
C、将摆线长当成了摆长 D、所用摆球的质量过大
E、把摆线长加上小球直径做为摆长
F、摆球在摆动过程中悬点出现了松动.

(1)用毫米尺量出悬线的长度L0=97.57cm,用游标卡尺测得摆球直径如图甲所示为d=
2.06
2.06
cm,则单摆的摆长为L=98.60
98.60
cm;以摆球通过平衡位置时开始计时,然后用秒表记录单摆完成全振动50次所用的时间,从图乙可读出时间为99.5
99.5
s,则单摆的周期为1.99
1.99
s.(2)根据记录的数据,在坐标纸上以T为纵轴,l为横轴,作出T-l图象,发现图线是曲线;然后尝试以T2为纵轴,l为横轴,作出T2-l图象,发现图线是一条过原点的倾斜直线,由此得出单摆做简谐运动的周期和摆长的关系是
D
D
A、T∝
| I | ||
|
| I |
| l |
(3)与重力加速度的真实值比较,发现测量结果偏小,分析原因可能是
BCF
BCF
A、振幅偏小 B、在单摆未悬挂之前先测定其摆长
C、将摆线长当成了摆长 D、所用摆球的质量过大
E、把摆线长加上小球直径做为摆长
F、摆球在摆动过程中悬点出现了松动.
分析:(1)考查游标卡尺和秒表的读数:先读主尺(只读整数),再加上游标尺(格数乘以分度分之一,格数找对齐的一个不估读),秒表:先读内圈,读数时只读整数,小数由外圈读出,读外圈时,指针是准确的,不用估读.
(2)由单摆周期公式的变形列出等式求解
(3)由单摆周期公式,求出重力加速度的表达式,根据重力加速度的表达式,分析重力加速度测量值偏小的原因.
(2)由单摆周期公式的变形列出等式求解
(3)由单摆周期公式,求出重力加速度的表达式,根据重力加速度的表达式,分析重力加速度测量值偏小的原因.
解答:解:(1)由图示游标卡尺可知,主尺的示数是2cm,游标尺的示数是6×0.1mm=0.6mm=0.06cm,
则游标卡尺示数,即小球直径d=2cm+0.06cm=2.06cm;
单摆摆长l=L0+
=98.60cm,
由图示秒表可知,分针示数是90s,秒针示数是9.5s,
秒表示数是90s+9.5s=99.5s,
单摆周期T=
=1.99s
(2)由单摆周期公式T=2π
变形得
T2=
l,所以T2-l图象应该是过原点的直线,
即做简谐运动的周期和摆长的关系是T2∝l,故选:D.
(3)根据单摆周期公式得重力加速度的表达式g=
,
A、重力加速度的测量值与振幅无关,故A错误;
B、在单摆未悬挂之前先测定其摆长,摆长偏小,g偏小,故B正确
C、将摆线长当成了摆长,摆长偏小,g偏小,故C正确
D、所用摆球的质量过大,不影响其重力加速度的测量值,故D错误
E、把摆线长加上小球直径做为摆长,摆长偏大,g偏大,故E错误
F、摆球在摆动过程中悬点出现了松动,使摆线长度增加了,摆长的测量值比实际值小,测得的g应偏小.故F正确
故选:BCF.
故答案为:①2.06;98.60cm; 99.5s; 1.99s. ②D ③BCF
则游标卡尺示数,即小球直径d=2cm+0.06cm=2.06cm;
单摆摆长l=L0+
| d |
| 2 |
由图示秒表可知,分针示数是90s,秒针示数是9.5s,
秒表示数是90s+9.5s=99.5s,
单摆周期T=
| t |
| n |
(2)由单摆周期公式T=2π
|
T2=
| 4π2 |
| g |
即做简谐运动的周期和摆长的关系是T2∝l,故选:D.
(3)根据单摆周期公式得重力加速度的表达式g=
| 4π2l |
| T2 |
A、重力加速度的测量值与振幅无关,故A错误;
B、在单摆未悬挂之前先测定其摆长,摆长偏小,g偏小,故B正确
C、将摆线长当成了摆长,摆长偏小,g偏小,故C正确
D、所用摆球的质量过大,不影响其重力加速度的测量值,故D错误
E、把摆线长加上小球直径做为摆长,摆长偏大,g偏大,故E错误
F、摆球在摆动过程中悬点出现了松动,使摆线长度增加了,摆长的测量值比实际值小,测得的g应偏小.故F正确
故选:BCF.
故答案为:①2.06;98.60cm; 99.5s; 1.99s. ②D ③BCF
点评:本题重点掌握单摆的周期公式,知道测量的原理,会正确确定摆长;能正确读取秒表的示数,会分析误差形成的原因.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 (2013?浙江模拟)在“探究单摆的周期与摆长的关系”的实验中,小明现在已经准备了中心有孔的小钢球、不易伸长的细线、铁架台及铁夹和游标卡尺.
(2013?浙江模拟)在“探究单摆的周期与摆长的关系”的实验中,小明现在已经准备了中心有孔的小钢球、不易伸长的细线、铁架台及铁夹和游标卡尺.