题目内容
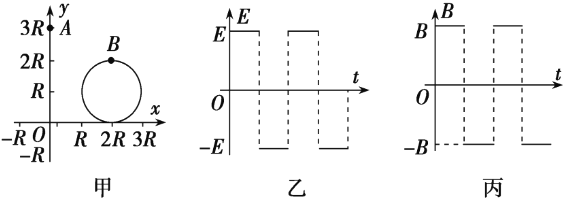
【题目】如图甲所示,在![]() 竖直平面内存在竖直方向的匀强电场,在第一象限内有一与x轴相切于点
竖直平面内存在竖直方向的匀强电场,在第一象限内有一与x轴相切于点![]() 、半径为R的圆形区域,该区域内存在垂直于
、半径为R的圆形区域,该区域内存在垂直于![]() 面的匀强磁场,电场与磁场随时间变化如图乙、丙所示,设电场强度竖直向下为正方向,磁场垂直纸面向里为正方向,电场、磁场同步周期性变化(每个周期内正、反向时间相同)。一带正电的小球A沿y轴方向下落,t=0时刻A落至点
面的匀强磁场,电场与磁场随时间变化如图乙、丙所示,设电场强度竖直向下为正方向,磁场垂直纸面向里为正方向,电场、磁场同步周期性变化(每个周期内正、反向时间相同)。一带正电的小球A沿y轴方向下落,t=0时刻A落至点![]() ,此时,另一带负电的小球B从圆形区域的最高点
,此时,另一带负电的小球B从圆形区域的最高点![]() 处开始在磁场内紧靠磁场边界做匀速圆周运动。当A球再下落R时,B球旋转半圈到达点
处开始在磁场内紧靠磁场边界做匀速圆周运动。当A球再下落R时,B球旋转半圈到达点![]() ;当A球到达原点O时,B球又旋转半圈回到最高点;然后A球开始做匀速运动。两球的质量均m,电荷量大小为q,不计空气阻力及两小球之间的作用力,重力加速度为g,求:
;当A球到达原点O时,B球又旋转半圈回到最高点;然后A球开始做匀速运动。两球的质量均m,电荷量大小为q,不计空气阻力及两小球之间的作用力,重力加速度为g,求:
(1)匀强电场的场强E的大小;
(2)小球B做匀速圆周运动的周期T及匀强磁场的磁感应强度B的大小;
(3)电场、磁场变化第一个周期末A、B两球间的距离S。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() R
R
【解析】
(1)小球 B 做匀速圆周运动,则重力和电场力平衡,洛伦兹力提供向心力,则有
Eq=mg,解得 ![]()
(2)设小球 B 的运动周期为 T,对小球 A:Eq+mg=ma,
解得 a=2g;
由 R=a(![]() )2,得
)2,得 ![]()
对 B 小球:![]()
![]()
解得![]()
(3)由题意分析可得:电(磁)场变化周期是 B 球做圆周运动周期的 2 倍
对小球 A:在原点的速度为![]() ,
,
在原点下的位移![]()
2T 末,小球 A的坐标为(0,-5R)
对小球B:球 B 的线速度 vB=π![]() ;
;
水平位移 xB=vBT=2πR;
竖直位移为 yB=![]() aT2=2R;
aT2=2R;
2T 末,小球B的坐标为[(2π+2)R,0]
则 2T 末,A、B两球的距离为: AB=![]() R。
R。

练习册系列答案
相关题目