题目内容
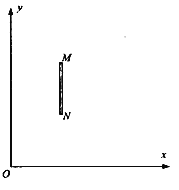
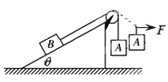
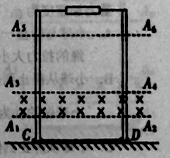
【题目】如图,一对表面粗糙的平行金属导轨固定在水平地面上,轨道与地面绝缘,轨道顶端连接有一定值电阻R,在![]() 、
、![]() 区域内有垂直轨道平面向里的匀强磁场,一水平金属杆CD通过两金属环套在轨道上,现使金属杆CD以某一初速度竖直向上运动,穿过磁场区域后继续上升到最高位置
区域内有垂直轨道平面向里的匀强磁场,一水平金属杆CD通过两金属环套在轨道上,现使金属杆CD以某一初速度竖直向上运动,穿过磁场区域后继续上升到最高位置![]() ,然后落回地面,此后不再运动,已知金属杆CD与轨道间的摩擦力大小恒为其重力的
,然后落回地面,此后不再运动,已知金属杆CD与轨道间的摩擦力大小恒为其重力的![]() 倍,金属杆CD向上运动经过
倍,金属杆CD向上运动经过![]() 和
和![]() 位置时的速度之比为2:1,
位置时的速度之比为2:1,![]() 与
与![]() 间的距离是
间的距离是![]() 与
与![]() 间的距离的n倍,金属杆CD向下运动刚进入磁场区域就座匀速运动,重力加速度为g,金属导轨与金属杆CD的电阻都忽略不计,求:
间的距离的n倍,金属杆CD向下运动刚进入磁场区域就座匀速运动,重力加速度为g,金属导轨与金属杆CD的电阻都忽略不计,求:
(1)金属杆CD向上、向下两次经过![]() 位置时的速度之比;
位置时的速度之比;
(2)金属杆CD向上运动经过![]() 刚进入磁场时的加速度大小;
刚进入磁场时的加速度大小;
(3)金属杆CD向上,向下两次经过磁场区域的过程中定值电阻R上产生的焦耳热之比。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
试题分析:(1)设杆的质量为m,![]() 与
与![]() 间的距离为h,上升过程中的加速度大小为
间的距离为h,上升过程中的加速度大小为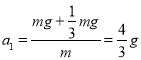
又![]() ,则
,则![]()
下降过程中的加速度大小为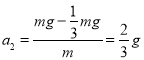
又![]() ,则
,则![]() ,即
,即![]()
(2)设杆的长度为![]() ,,杆上下运动经过
,,杆上下运动经过![]() 时的速度为
时的速度为![]() ,切割产生的电动势
,切割产生的电动势![]()
回路中的电流![]()
杆受到的安培力大小为![]() ,方向竖直向下
,方向竖直向下
杆向上运动经过![]() 刚进入磁场时,由牛顿第二定律可得:
刚进入磁场时,由牛顿第二定律可得:![]()
解得![]()
由题意,杆下落进入磁场做匀速运动的速度为![]()
切割产生的电动势![]()
此时回路中的电流![]()
杆受到的安培力大小为![]()
这一过程中杆受力平衡,即![]()
可得![]()
因为![]() ,又
,又![]() ,可得
,可得![]()
代入可得![]()
(3)设![]() 与
与![]() 间的距离为d,杆向上穿过磁场的过程中,由动能定理
间的距离为d,杆向上穿过磁场的过程中,由动能定理![]()
杆过![]() 后继续上升了nd,这一过程由动能定理:
后继续上升了nd,这一过程由动能定理:![]()
杆下落过程中,![]()
由功能关系有![]()
即![]()

练习册系列答案
相关题目