题目内容
(2008?黄冈模拟)如图为示波管的部分示意图,竖直YY′和水平XX′偏转电极的板车都为l=4cm,电极间距离都为d=1cm,YY′、XX′板右端到荧光屏的距离分别为10cm和12cm,两偏转电场间无相互影响.电子束通过A板上的小孔沿中心轴线进入偏转电极时的速度为v0=1.6×107m/s,元电荷电量e=1.6×10-19C,电子质量m=0.91×10-39kg.当偏转电极上不加电压时,电子束打在荧光屏上的O点.求:
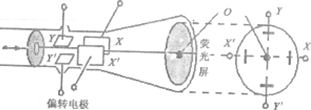
(1)要使电子束不打在偏转电极的极板上,加在偏转电极上的偏转电压U不能超过多大?
(2)若在偏转电极XX′上加Ux=45.5sin(10πt)V的电压,在偏转电极YY′上加Uy=45.5cos(100πt)V的电压,通过计算说明源源不断的电子灯打在荧光屏上所产生亮点的轨迹形状.

(1)要使电子束不打在偏转电极的极板上,加在偏转电极上的偏转电压U不能超过多大?
(2)若在偏转电极XX′上加Ux=45.5sin(10πt)V的电压,在偏转电极YY′上加Uy=45.5cos(100πt)V的电压,通过计算说明源源不断的电子灯打在荧光屏上所产生亮点的轨迹形状.
分析:(1)粒子在偏转电场中做类平抛运动,抓住沿电场方向做初速度为零的匀加速直线运动,垂直电场方向做匀速直线运动,抓住偏转位移的最大值为
,结合牛顿第二定律和运动学公式,通过等时性求出偏转电压的最大值.
(2)电场的变化周期远大于粒子在偏转电场中运动的时间,可以认为电子通过偏转电场的过程中板间时均为匀强电场,抓住粒子出偏转电场时速度的反向延长线经过中轴线的中点,根据相似三角形求出打在荧光屏上距离O点的距离,从而得出x和y坐标的关系式,确定轨迹的形状.
| d |
| 2 |
(2)电场的变化周期远大于粒子在偏转电场中运动的时间,可以认为电子通过偏转电场的过程中板间时均为匀强电场,抓住粒子出偏转电场时速度的反向延长线经过中轴线的中点,根据相似三角形求出打在荧光屏上距离O点的距离,从而得出x和y坐标的关系式,确定轨迹的形状.
解答:解:(1)设偏转电场的场强为E,则有:E=
①
设电子经时间t通过偏转电场,偏离轴线的侧向位移为s侧,则有:
在中心轴线方向上:t=
②
在轴线侧向有:a=
③
S侧=
at2④
要使电子束不打在偏转电极的极板上,则
≥S侧⑤
代入数据解①~⑤式可得U≤91V
(2)由②式可得t=2.5×10-9s
而电场的变化周期T=
得T=0.02s≥t
故可以认为电子通过偏转电场的过程中板间时均为匀强电场
设电子通过偏转电场过程中产生的侧向速度为v侧,偏转角为θ,则电子通过偏转电场时有:v侧=a?t⑥
tanθ=
⑦
设偏转极板右端到荧光屏距离为L,因为粒子出电场时速度的反向延长线经过中轴线的中点.
根据相似三角形得,
=
=tanθ
电子在荧光屏上偏离O点的距离为s=(
+L)tanθ⑧
由①~③式、⑥~⑨式可得电子在荧光屏上的x、y坐标为:x=0.018sin(100πt)my=0.025cos(100πt)m
所以荧光屏上出现的是半长轴和半短轴分别为0.025m、0.018m的椭圆.
答:(1)加在偏转电极上的偏转电压U不能超过91V.
(2)荧光屏上出现的是半长轴和半短轴分别为0.025m、0.018m的椭圆.
| U |
| d |
设电子经时间t通过偏转电场,偏离轴线的侧向位移为s侧,则有:
在中心轴线方向上:t=
| l |
| v0 |
在轴线侧向有:a=
| eE |
| m |
S侧=
| 1 |
| 2 |
要使电子束不打在偏转电极的极板上,则
| d |
| 2 |
代入数据解①~⑤式可得U≤91V
(2)由②式可得t=2.5×10-9s
而电场的变化周期T=
| 2π |
| ω |
故可以认为电子通过偏转电场的过程中板间时均为匀强电场
设电子通过偏转电场过程中产生的侧向速度为v侧,偏转角为θ,则电子通过偏转电场时有:v侧=a?t⑥
tanθ=
| v侧 |
| v0 |
设偏转极板右端到荧光屏距离为L,因为粒子出电场时速度的反向延长线经过中轴线的中点.
根据相似三角形得,
| s侧 |
| s |
| ||
|
电子在荧光屏上偏离O点的距离为s=(
| l |
| 2 |
由①~③式、⑥~⑨式可得电子在荧光屏上的x、y坐标为:x=0.018sin(100πt)my=0.025cos(100πt)m
所以荧光屏上出现的是半长轴和半短轴分别为0.025m、0.018m的椭圆.
答:(1)加在偏转电极上的偏转电压U不能超过91V.
(2)荧光屏上出现的是半长轴和半短轴分别为0.025m、0.018m的椭圆.
点评:本题考查带电粒子在电场中的偏转,掌握处理曲线运动的方法,知道粒子在沿电场方向做初速度为零的匀加速直线运动,垂直电场方向做匀速直线运动.

练习册系列答案
相关题目
 (2008?黄冈模拟)彩虹产生的原因是由阳光射入雨滴(视为球形)时,经一次反射和两次折射而产生色散形成的.如图所示为太阳光射到空气中的小水珠发生色散形成彩虹的光路示意图,a、b为两种单色光的出射光线.以下说法正确的是( )
(2008?黄冈模拟)彩虹产生的原因是由阳光射入雨滴(视为球形)时,经一次反射和两次折射而产生色散形成的.如图所示为太阳光射到空气中的小水珠发生色散形成彩虹的光路示意图,a、b为两种单色光的出射光线.以下说法正确的是( ) (2008?黄冈模拟)如图所示,在光滑水平面上直线MN右侧有垂直于水平面的匀强磁场,一个电阻为R的矩形线框abcd受到水平向左的恒定拉力作用,以一定的初速度向右进入磁场,经过一段时间后又向左离开磁场.在整个运动过程中ab边始终平行于MN.则线框向右运动进入磁场和向左运动离开磁场这两个过程中( )
(2008?黄冈模拟)如图所示,在光滑水平面上直线MN右侧有垂直于水平面的匀强磁场,一个电阻为R的矩形线框abcd受到水平向左的恒定拉力作用,以一定的初速度向右进入磁场,经过一段时间后又向左离开磁场.在整个运动过程中ab边始终平行于MN.则线框向右运动进入磁场和向左运动离开磁场这两个过程中( ) (2008?黄冈模拟)两根光滑的足够长直金属导轨MN、M′N′平行置于竖直面内,导轨间距为l,导轨上端接有阻值为R的电阻,如图所示.质量为m、长度也为l、阻值为r的金属棒ab垂直于导轨放置,且与导轨保持良好接触,其他电阻不计.导轨处于磁感应强度为B、方向水平向里的匀强磁场中,ab由静止释放,在重力作用下向下运动,求:
(2008?黄冈模拟)两根光滑的足够长直金属导轨MN、M′N′平行置于竖直面内,导轨间距为l,导轨上端接有阻值为R的电阻,如图所示.质量为m、长度也为l、阻值为r的金属棒ab垂直于导轨放置,且与导轨保持良好接触,其他电阻不计.导轨处于磁感应强度为B、方向水平向里的匀强磁场中,ab由静止释放,在重力作用下向下运动,求: (2008?黄冈模拟)如图为一列简谐横波在某一时刻的波形图象,图中P1、P2、P3分别表示介质中三个质点A、B、C在该时刻的振动状态.已知波沿x轴正方向传播,波速v=20m/s,下列说法中正确的是( )
(2008?黄冈模拟)如图为一列简谐横波在某一时刻的波形图象,图中P1、P2、P3分别表示介质中三个质点A、B、C在该时刻的振动状态.已知波沿x轴正方向传播,波速v=20m/s,下列说法中正确的是( ) (2008?黄冈模拟)如图所示,两光屏间放有两个偏振片,它们四者平行共轴,现让太阳光沿轴线通过光屏M上的小孔照射到固定不动的偏振片P上,再使偏振片Q绕轴匀速转动一周,则关于光屏上光的亮度变化情况,下列说法中正确的是( )
(2008?黄冈模拟)如图所示,两光屏间放有两个偏振片,它们四者平行共轴,现让太阳光沿轴线通过光屏M上的小孔照射到固定不动的偏振片P上,再使偏振片Q绕轴匀速转动一周,则关于光屏上光的亮度变化情况,下列说法中正确的是( )