题目内容
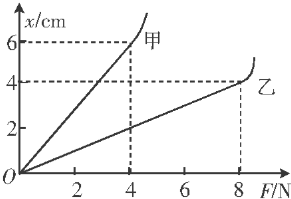
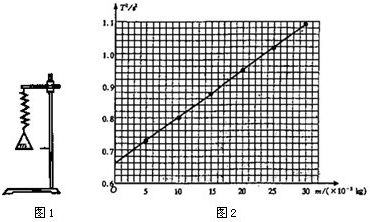
(10分)如图所示,一个弹簧台秤的秤盘质量和弹簧质量都可以不计,盘内放一个物体P处于静止。P的质量为12kg,弹簧的劲度系数k=800N/m。现给P施加一个竖直向上的力F,使P从静止开始向上做匀加速运动。已知在前0.2s内F是变化的,在0.2s以后F是恒力,则F的最小值是多少,最大值是多少?
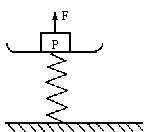
解析:解题的关键是要理解0.2s前F是变力,0.2s后F是恒力的隐含条件。即在0.2s前物体受力和0.2s以后受力有较大的变化。
以物体P为研究对象。物体P静止时受重力G、称盘给的支持力N。
因为物体静止,∑F=0
N=G= 0 ①
N=kx0 ②
设物体向上匀加速运动加速度为a。
此时物体P受力如图所示,受重力G,拉力F和支持力N′
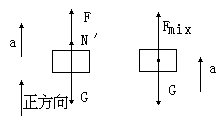
据牛顿第二定律有
F+N′-G = ma ③
当0.2s后物体所受拉力F为恒力,即为P与盘脱离,即弹簧无形变,由0~0.2s内物体的位移为x0。物体由静止开始运动,则
![]() ④
④
将式①,②代入④中解得的x0= 0.15m
代入式③解得a=7.5m/s2
F的最小值由式③可以看出即N′最大时,即初始时刻N′=N = kx。
代入式③得
Fmin= ma + mg-kx0=12×(7.5+10)-800×0.15=90(N)
F最大值即N=0时,F = ma+mg = 210(N)
错解分析:错解:
F最大值即N=0时,F=ma+mg=210(N)
错解原因是对题所叙述的过程不理解。把平衡时的关系G=F+N,不自觉的贯穿在解题中。

练习册系列答案
相关题目
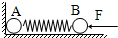 质量均为m的A、B两个小球之间系一个质量不计的弹簧,放在光滑的台面上.A紧靠墙壁,如图所示,今用恒力F将B球向左挤压弹簧,达到平衡时,突然将力撤去,此瞬间( )
质量均为m的A、B两个小球之间系一个质量不计的弹簧,放在光滑的台面上.A紧靠墙壁,如图所示,今用恒力F将B球向左挤压弹簧,达到平衡时,突然将力撤去,此瞬间( )A、A球的加速度为
| ||
| B、A球的加速度为零 | ||
C、B球的加速度为
| ||
D、B球的加速度为
|
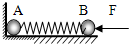 A、B两球质量均为m,它们之间系一个轻弹簧,放在光滑的台面上,A球靠墙壁,如图所示.如果用力F将B球压缩弹簧,平衡后,突然撤去F,则在这瞬间( )
A、B两球质量均为m,它们之间系一个轻弹簧,放在光滑的台面上,A球靠墙壁,如图所示.如果用力F将B球压缩弹簧,平衡后,突然撤去F,则在这瞬间( ) (2012?山西一模)在“探究弹力与弹簧伸长的关系”的实验中.
(2012?山西一模)在“探究弹力与弹簧伸长的关系”的实验中.