题目内容
10．
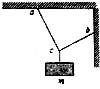用三根轻绳将质量为2m的物块悬挂在空中，如图所示，已知ac和bc与竖直方向的夹角分别为30°和60°，则ac绳和bc绳的拉力分别为（ ）| A． | A、$\sqrt{3}$mg，mg | B． | mg，$\sqrt{3}$mg | C． | $\frac{\sqrt{3}}{2}$mg，$\frac{1}{2}$mg | D． | $\frac{1}{2}$mg，$\frac{\sqrt{3}}{2}$mg |
分析 对c点进行受力分析，然后根据平衡条件和三角函数表示出力与力之间的关系．
解答 解：对结点C受力分析，受到三根绳子拉力，将Fa和Fb合成为F，
根据三力平衡得出：F=Fc=2mg
已知ac和bc与竖直方向的夹角分别为30°和60°，所以α=30°
根据三角函数关系得出：
Fa=F•cosα=$\frac{\sqrt{3}}{2}$•2mg=$\sqrt{3}mg$
Fb=F•sinα=$\frac{1}{2}$•2mg=mg
故选：A．
点评 该题的关键在于能够对结点c进行受力分析，利用平衡状态条件解决问题；力的计算离不开几何关系和三角函数．
练习册系列答案
相关题目
20．如图，在真空中把一绝缘导体向带负电的小球缓慢地靠近，下列说法中正确的是（ ）
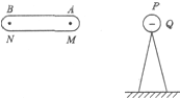
| A． | b端的感应电荷越来越少 | |
| B． | 导体内场强越来越大 | |
| C． | 导体的感应电荷在M点产生的场强恒大于在N点产生的场强 | |
| D． | 导体的感应电荷在M、N两点的场强相等 |
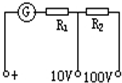如图所示是一个双量程电压表，表头是一个内阻Rg=500Ω，满刻度电流为Ig=10mA的毫安表，现接成量程分别为10V和100V的两个量程，则所串联的电阻R1=500Ω，R2=9000Ω．
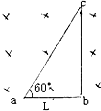如图所示，一个直角三角形导线框放在匀强磁场中，磁场方向垂直线框平面指向纸内，磁感应强度为B，ab=L．当线框绕过b点的轴在纸面上顺时针以角速度ω转动时，线框中的感应电流大小为0，ca两点的电势差为φca=BL2ω．
15．
某次军事演习中，红方飞机甲正从北向南水平匀速飞行，飞行员发现其正前方距离x处有一架蓝方飞机乙正从东向匀速飞行，随即水平发射炮弹，炮弹的发射方向与飞机的飞行方向成θ角，经过时间t炮弹击中飞机乙．已知飞机甲的速度为v1，乙的速度为v2，甲在地面上静止时发射炮弹的速度为v0．忽略炮弹竖直方向的位移和所受的空气阻力．则下列说法中正确的是（ ）
某次军事演习中，红方飞机甲正从北向南水平匀速飞行，飞行员发现其正前方距离x处有一架蓝方飞机乙正从东向匀速飞行，随即水平发射炮弹，炮弹的发射方向与飞机的飞行方向成θ角，经过时间t炮弹击中飞机乙．已知飞机甲的速度为v1，乙的速度为v2，甲在地面上静止时发射炮弹的速度为v0．忽略炮弹竖直方向的位移和所受的空气阻力．则下列说法中正确的是（ ）| A． | tan=$\frac{{v}_{2}}{{v}_{1}}$ | B． | sinθ=$\frac{{v}_{2}}{{v}_{1}}$ | ||
| C． | t=$\frac{x}{\sqrt{{{v}_{0}}^{2}-{{v}_{2}}^{2}}+{v}_{1}}$ | D． | t=$\frac{x}{{v}_{1}}$ |
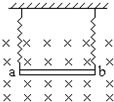如图所示，一粗细均匀、重1N的金属丝ab，两端用相同的轻弹簧挂起（弹簧下端与金属丝绝缘），放在一方向垂直于纸面向里的匀强磁场（匀强磁场的范围足够大）中，若在金属丝中通入大小为I、方向自a至b的电流，此时所受安培力的大小为0.5N，金属丝下降1mm；则金属丝受的弹力为0.5N，若改在金属丝中通入大小仍为I但方向自b至a的电流，金属丝应下降3mm．