题目内容
10.如图甲所示,MNCD为一足够长的光滑绝缘斜面,EFGH范围内存在方向垂直斜面向下的匀强磁场,磁场边界EF、HG与斜面底边MN(在水平面内)平行.一正方形金属框abcd放在斜面上,ab边平行于磁场边界.现使金属框从斜面上某处由静止释放,金属框从开始运动到cd边离开磁场的过程中,其运动的v-t图象如图乙所示.已知金属框电阻为R,质量为m,重力加速度为g,图乙中金属框运动的各个时刻及对应的速度均为已知量,求:
(1)磁场区域的宽度d;
(2)金属框穿过磁场过程中产生的焦耳热Q热.
分析 (1)磁场区域的宽度d等于金属框ab边在t1至3t1时间内运动位移的大小,根据v-t图象的面积求解.
(2)由速度图象读出加速度,由牛顿第二定律求出斜面倾角的正弦值.线框从t1时刻进入磁场到t2时刻离开磁场,金属框穿过磁场过程中机械能减小转化为内能,根据能量守恒定律求出焦耳热.
解答 解:(1)根据金属框运动的v-t图象可知,金属框ab边在t1时刻开始进入磁场区域,在t1至2t1时间内金属框做速度大小为v1的匀速直线运动,金属框cd边在2t1时刻开始进入磁场区域,在2t1至3t1时间内金属框做匀加速直线运动,在3t1时刻,金属框ab边离开磁场区域.
则磁场区域的宽度d等于金属框ab边在t1至3t1时间内运动位移的大小,根据v-t图象得:
$d={v_1}{t_1}+\frac{{({{v_1}+2{v_1}})({3{t_1}-2{t_1}})}}{2}$…①
解得:$d=\frac{{5{v_1}{t_1}}}{2}$…②
(2)设光滑绝缘斜面的倾角为θ,正方形金属框的边长为l,在金属框ab边从t1时刻进入磁场到金属框cd边从t2时刻离开磁场的过程中,由功能关系得:$mg(d+l)sinθ=\frac{1}{2}m{v_2}^2-\frac{1}{2}m{v_1}^2+Q$热…③
根据金属框运动的v-t图象可知,金属框ab边在t1时刻开始进入磁场区域,在t1至2t1时间内金属框做速度大小为v1的匀速直线运动,则有:
l=v1t1…④
根据v-t图象可知,在0至t1时间内金属框做初速度为零的匀加速直线运动,又根据牛顿第二定律得:
$mgsinθ=ma=m\frac{v_1}{t_1}$…⑤
由①~⑤解得:Q热=$4m{v}_{1}^{2}-\frac{1}{2}m{v}_{2}^{2}$…⑥
答:(1)磁场区域的宽度d是$\frac{5{v}_{1}{t}_{1}}{2}$;
(2)金属框穿过磁场过程中产生的焦耳热Q热是$4m{v}_{1}^{2}-\frac{1}{2}m{v}_{2}^{2}$.
点评 本题除了考查电磁感应知识外,着重考查对速度图象的识别、理解能力,要充分挖掘图象的信息,如“面积”“斜率”等表示的意义.

 阅读快车系列答案
阅读快车系列答案 用三根轻绳将质量为2m的物块悬挂在空中,如图所示,已知ac和bc与竖直方向的夹角分别为30°和60°,则ac绳和bc绳的拉力分别为( )
用三根轻绳将质量为2m的物块悬挂在空中,如图所示,已知ac和bc与竖直方向的夹角分别为30°和60°,则ac绳和bc绳的拉力分别为( )| A. | A、$\sqrt{3}$mg,mg | B. | mg,$\sqrt{3}$mg | C. | $\frac{\sqrt{3}}{2}$mg,$\frac{1}{2}$mg | D. | $\frac{1}{2}$mg,$\frac{\sqrt{3}}{2}$mg |
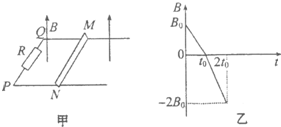 如图甲所示,导体棒MN置于水平导轨上,PQMN所围的面积为S,PQ之间有阻值为R的电阻,不计导轨和导体棒的电阻.导轨所在区域内存在沿竖直方向的匀强磁场,规定磁场方向竖直向上为正,在0~2t0时间内磁感应强度的变化情况如图乙所示,导体棒MN始终处于静止状态.下列说法正确的是( )
如图甲所示,导体棒MN置于水平导轨上,PQMN所围的面积为S,PQ之间有阻值为R的电阻,不计导轨和导体棒的电阻.导轨所在区域内存在沿竖直方向的匀强磁场,规定磁场方向竖直向上为正,在0~2t0时间内磁感应强度的变化情况如图乙所示,导体棒MN始终处于静止状态.下列说法正确的是( )| A. | 在0~t0和t0~2t0时间内,导体棒中电流方向相同 | |
| B. | 在0~t0和t0~2t0时间内,导体棒受到的摩擦力方向相同 | |
| C. | 在t0~2t0内,通过电阻R的电流大小为$\frac{S{B}_{0}}{R{t}_{0}}$ | |
| D. | 在0~2t0时间内,通过电阻R的电荷量为$\frac{3{B}_{0}S}{R}$ |
| A. | 一个周期内,振动在介质中传播的距离等于一个波长 | |
| B. | 一个周期内,介质中的质点通过的路程等于一个波长 | |
| C. | 波长等于在波的传播方向上振动相位总是相同的两个质点间的距离 | |
| D. | 波长等于波峰与波谷间距离的2倍 |
| A. | 灯管点燃发光后,启动器中两触片是分离的 | |
| B. | 镇流器起整流作用 | |
| C. | 灯管点燃发光后,镇流器起降压限流作用 | |
| D. | 镇流器给日光灯开始点燃时提供瞬时高压 |
 如图所示,竖直平面内有一半径为r、电阻为R1、粗细均匀的光滑半圆形金属环,在M、N处与距离为2r、电阻不计的平行光滑金属导轨ME、NF相接,EF之间接有电阻R2,已知R1=12R,R2=4R.在MN上方及CD下方有水平方向的匀强磁场I和II,磁感应强度大小均为B.现有质量为m、电阻不计的导体棒ab从半圆环的最高点A处由静止下落,在下落过程中导体棒始终保持水平,与半圆形金属环及轨道接触良好,设平行导轨足够长.已知导体棒下落0.5r时的速度大小为v1,下落到MN处时的速度大小为v2.不计空气阻力,重力加速度为g.
如图所示,竖直平面内有一半径为r、电阻为R1、粗细均匀的光滑半圆形金属环,在M、N处与距离为2r、电阻不计的平行光滑金属导轨ME、NF相接,EF之间接有电阻R2,已知R1=12R,R2=4R.在MN上方及CD下方有水平方向的匀强磁场I和II,磁感应强度大小均为B.现有质量为m、电阻不计的导体棒ab从半圆环的最高点A处由静止下落,在下落过程中导体棒始终保持水平,与半圆形金属环及轨道接触良好,设平行导轨足够长.已知导体棒下落0.5r时的速度大小为v1,下落到MN处时的速度大小为v2.不计空气阻力,重力加速度为g.
