��Ŀ����
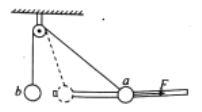
����Ŀ��2022�궬�»Ὣ�ڱ������У���ʱ�������ྫ�ʴ̼��ı����������ɽ��ѩU�γؾ�������֮һ�����ij����dz�Լ120�ף���Ϊ4.5�ף��� 15��U�λ�����������ֱѩ����ص�ѩ����Բ��ѩ��������ɣ��������U����״��������������ƽ���¶�18����ѡ���ڸߴ��������U�γ�һ���Ե��ʾ��ͼ��A�㣩������������U�ͳػ�������һ����ֱ�������B��Ծ���ڿ�����������ץ����ת�ȶ�������ɶ����������ٻ���Բ࣬��˷���Ծ������ѶȲ�ͬ�Ķ�����ֱ������������ɱ��������и���ѡ����ɶ���������Ч����֡�

��1��ѡ�ֳ���ʱҪ�Ⱦ���һ����б�µ����������龰ͼ�������¶����Ϊ����������ѩ��Ķ�Ħ������Ϊ�������ص��������ٶ�Ϊg����ѡ���ش�б���µ����»��еļ��ٶȴ�С��
��2���ڸ�������ѧϰ�У����ڸ��ӵ��˶��������÷ֽ���о������������ƽ���˶����о���
a���˶�Ա��U�γش�A���е�B�Ĺ�����һ�����ӵ��˶��������÷ֽ�ķ������о�����˶�����������ķֽ�����
b..��ƽ�����»��ϣ���������Ф��������������ԵԾ��ʱ����ת1440����������Ϊ����ת���ܣ������ѶȵĶ�����ø���Ŀ�Ĺھ���Ϊ�˼��Դﵽ���ض��������⣬�˹�����������Ϊ�ʵ㣬��ÿתһ����С��ʱ0.5�룬������ʱ�ٶ�����ֱ������ͬһƽ���ڣ�����ֱ���ϵļн�Ϊ20�������䵽��������ͬһ�߶�ǰҪ���ȫ��������ȫ���̺��Կ���������������������С�ٶ�Ϊ���٣�
��gȡ10m/s2 sin20��=0.34 cos20��=0.94��
���𰸡���1��gsin������gcos����2��a�����Խ����˶��ػ����¶ȷ����U�ͽ��淽��ֽ⣻���µ��������������ֱ���ȼ���ֱ���˶����ؽ��淽�������������˶���Բ���˶����ȼ���ֱ���˶�����ֱ�����˶���b..����������С�ٶ�Ϊ10.6m/s
���������⣺��1������������ͼ����mg�ֽ�
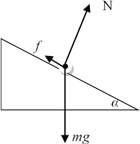
��ţ�ٵڶ����ɣ�mgsin��- f = ma
����Ħ���� f = ��mgcos��
�ó� a = gsin�� - ��gcos��
��2��a. ���Խ����˶��ػ����¶ȷ����U�ͽ��淽��ֽ⣻
���µ��������������ֱ���ȼ���ֱ���˶���
�ؽ��淽�������������˶���Բ���˶����ȼ���ֱ���˶�����ֱ�����˶���
b. ��������ʱT=2s
��ѡ�ֵ��˶��ֽ�Ϊˮƽ����ֱ�������˶�����ֱ�������ȱ���ֱ���˶���
���������˶�ʱ�� T1 = t/2 = 1s
����ʱ�ٶȵ���ֱ���� vy = gt1 = 10m/s
����ʱ��С�ٶ� v=vy/cos��=10.6m/s