Question

【题目】如图（甲）所示，一根轻绳上端固定在O点，下端拴一个重为G的钢球A，球处于静止状态，现对球施加一个方向向右的外力F，使球缓慢偏移，在移动中的每一时刻，都可以认为球处于平衡状态，如果外力F方向始终水平，最大值为2G，试求：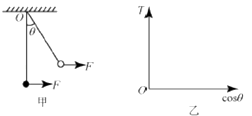

（1）轻绳张力T的大小取值范围；
（2）求出轻绳的张力T与cosθ的关系，并在图（乙）中画出T与cosθ的关系图象．

Answer 1

【答案】
（1）解：对小球，画出受力分析，如图所示：

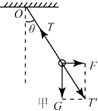
由图可知， ，

F在0﹣2G之间变化，T的取值范围为[G， G]；

答：轻绳张力T的大小取值范围为[G， G]

（2）解：小球竖直方向受力平衡，故：Tcos0﹣mg=0，

即 ，

图象如图所示：

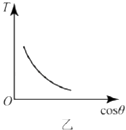
答：轻绳的张力T与cosθ的关系为 ，T与cosθ的关系图象如图所示．

【解析】（1）对小球受力分析，受水平拉力F、重力和细线的拉力，根据平衡条件列式求解；（2）根据平衡条件并采用正交分解法列式求解出T与cosθ的关系表达式后作图．
【考点精析】通过灵活运用力的合成和力的分解，掌握求几个已知力的合力，叫做力的合成；共点的两个力（F 1 和F 2 ）合力大小F的取值范围为:|F 1 -F 2 |≤F≤F 1 +F 2；求一个已知力的分力，叫做力的分解（力的分解与力的合成互为逆运算）；在实际问题中，通常将已知力按力产生的实际作用效果分解;为方便某些问题的研究，在很多问题中都采用正交分解法即可以解答此题．