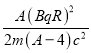题目内容
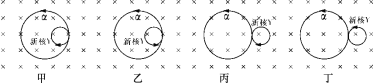
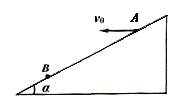
【题目】如图所示,半径为r的圆形匀强磁场区域Ⅰ与x轴相切于坐标系的原点O,磁感应强度为B0,方向垂直于纸面向外.磁场区域Ⅰ右侧有一长方体加速管,加速管底面宽度为2r,轴线与x轴平行且过磁场区域Ⅰ的圆心,左侧的电势比右侧高.在加速管出口下侧距离2r处放置一宽度为2r的荧光屏.加速管右侧存在方向垂直于纸面向外磁感应强度也为B0的匀强磁场区域Ⅱ.在O点处有一个粒子源,能沿纸面向y>0的各个方向均匀地发射大量质量为m、带电荷量为q且速率相同的粒子,其中沿y轴正方向射入磁场的粒子,恰能沿轴线进入长方形加速管并打在荧光屏的中心位置.(不计粒子重力及其相互作用)
(1)求粒子刚进入加速管时的速度大小v0;
(2)求加速电压U;
(3)若保持加速电压U不变,磁场Ⅱ的磁感应强度B=0.9 B0,求荧光屏上有粒子到达的范围?
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
由运动方向通过几何关系求得半径,进而由洛伦兹力作向心力求得速度;再由几何关系求得半径,由洛伦兹力作向心力联立两式求得粒子速度,应用动能定理求得加速电压;先通过几何关系求得粒子在加速管中的分布,然后由粒子运动的半径及几何关系求得可打在荧光屏上的粒子范围;
解:(1)磁场区域Ⅰ内粒子运动轨道半径为:![]()
![]()
![]()
(2)粒子在磁场区域Ⅱ的轨道半径为: ![]()
![]()
又![]()
![]()
由动能定理得:![]()
解得:![]()
(3)粒子经磁场区域Ⅰ后,其速度方向均与x轴平行;经证明可知: OO1CO2是菱形,所以CO2和y轴平行,v和x轴平行

磁场Ⅱ的磁感应强度B2减小10%,即 ![]() ,
,![]()
荧光屏上方没有粒子到达的长度为:![]()
即荧光屏上有粒子到达的范围是:距上端![]() 处到下端,总长度
处到下端,总长度![]()

【题目】某物理兴趣小组在“探究弹性势能的表达式”的实验中,用一个被压缩的弹簧沿粗糙水平面弹出一个小物体,测得弹簧被压缩的距离![]() 和小物体在粗糙水平面上滑动的距离
和小物体在粗糙水平面上滑动的距离![]() 如下表所示。
如下表所示。
实验次数 | 1 | 2 | 3 | 4 |
d/cm | 1.00 | 2.00 | 3.00 | 4.00 |
x/m | 1.00 | 4.02 | 9.01 | 16.02 |
(1)由此表可以归纳出,小物体滑动的距离![]() 与弹簧被压缩的距离
与弹簧被压缩的距离![]() 之间的关系为x=___(式中的常量用
之间的关系为x=___(式中的常量用![]() 表示)。
表示)。
(2)弹簧的弹性势能![]() 与弹簧被压缩的距离
与弹簧被压缩的距离![]() 之间的关系为
之间的关系为![]() =____ (式中的常量用k2表示)。
=____ (式中的常量用k2表示)。