题目内容
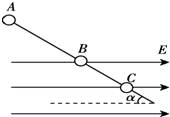 如图所示,一根光滑绝缘细杆与水平面成α=30°的角倾斜固定.细杆的一部分处在场强方向水平向右的匀强电场中,场强E=2×104N/C.在细杆上套有一个带电荷量为q=-1.73×10-5C、质量为m=3×10-2kg的小球.现使小球从细杆的顶端A由静止开始沿杆滑下,并从B点进入电场,小球在电场中滑至最远处的C点.已知A、B间的距离x1=0.4m,g=10m/s2.求:
如图所示,一根光滑绝缘细杆与水平面成α=30°的角倾斜固定.细杆的一部分处在场强方向水平向右的匀强电场中,场强E=2×104N/C.在细杆上套有一个带电荷量为q=-1.73×10-5C、质量为m=3×10-2kg的小球.现使小球从细杆的顶端A由静止开始沿杆滑下,并从B点进入电场,小球在电场中滑至最远处的C点.已知A、B间的距离x1=0.4m,g=10m/s2.求:(1)小球在B点的速度vB;
(2)小球进入电场后滑行的最大距离x2;
(3)小球从A点滑至C点所用的时间t.
分析:分段应用动能定理列出等式求解小球在B点的速度,对于整个过程,运用动能定理列式,即可求得小球进入电场后滑行的距离.
在AB段只有重力做功,BC段重力和电场力都做功.
在AB段只有重力做功,BC段重力和电场力都做功.
解答:解:(1)由A到B,根据动能定理列出等式:
mgx1sinα=
m
代入数据解得VB=2m/s
(2)小球从细杆的顶端A由静止开始沿杆滑下,并从B点进入电场,小球在电场中滑至最远处的C点,滑行到C点速度为零.
对于小球的整个滑行过程,由动能定理得:
mg(x1+x2)sinα-qEx2cosα=0
则得 x2=0.4m,
(3)根据运动学公式得:
x1+x2=
×tAB+
×tBC,
而总时间 t=tAB+tBC,
解得:t=0.8s,
答:(1)小球在B点的速度大小是2m/s;
(2)小球进入电场后滑行的最大距离是0.4m;
(3)小球从A点滑至C点所用的时间是0.8s.
mgx1sinα=
| 1 |
| 2 |
| v | 2 B |
代入数据解得VB=2m/s
(2)小球从细杆的顶端A由静止开始沿杆滑下,并从B点进入电场,小球在电场中滑至最远处的C点,滑行到C点速度为零.
对于小球的整个滑行过程,由动能定理得:
mg(x1+x2)sinα-qEx2cosα=0
则得 x2=0.4m,
(3)根据运动学公式得:
x1+x2=
| 0+v |
| 2 |
| v+0 |
| 2 |
而总时间 t=tAB+tBC,
解得:t=0.8s,
答:(1)小球在B点的速度大小是2m/s;
(2)小球进入电场后滑行的最大距离是0.4m;
(3)小球从A点滑至C点所用的时间是0.8s.
点评:本题考查了动能定理的应用,注意分析在全过程中哪些力对物体做功,是正功还是负功.
涉及力在空间的效果,运用动能定理求解距离比较简单方便,运用平均速度求时间比较简便.也可以根据牛顿第二定律和运动学公式结合求解.
涉及力在空间的效果,运用动能定理求解距离比较简单方便,运用平均速度求时间比较简便.也可以根据牛顿第二定律和运动学公式结合求解.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
 如图所示,一气缸竖直放置,用一质量为m的活塞在缸内封闭了一定量的理想气体,在气缸的底部安装有一根电热丝,用导线和外界电源相连,已知气缸壁和活塞都是绝热的,气缸壁与活塞间接触光滑且不漏气.现接通电源,电热丝对缸内气体缓慢加热.设活塞横截面积为S,外界大气压强为p0,电热丝热功率为P,测得通电t时间内活塞缓慢向上移动高度h,求:
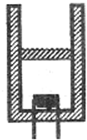
如图所示,一气缸竖直放置,用一质量为m的活塞在缸内封闭了一定量的理想气体,在气缸的底部安装有一根电热丝,用导线和外界电源相连,已知气缸壁和活塞都是绝热的,气缸壁与活塞间接触光滑且不漏气.现接通电源,电热丝对缸内气体缓慢加热.设活塞横截面积为S,外界大气压强为p0,电热丝热功率为P,测得通电t时间内活塞缓慢向上移动高度h,求: (1)如图所示,一汽缸竖直放置,用一质量为m的活塞在缸内封闭了一定量的理想气体,在气缸的底部安装有一根电热丝,用导线和外界电源相连,已知气缸壁和活塞都是绝热的,气缸壁与活塞间接触光滑且不漏气,现接通电源,电热丝对缸内气体缓慢加热.关于气缸内气体,下列说法正确的是
(1)如图所示,一汽缸竖直放置,用一质量为m的活塞在缸内封闭了一定量的理想气体,在气缸的底部安装有一根电热丝,用导线和外界电源相连,已知气缸壁和活塞都是绝热的,气缸壁与活塞间接触光滑且不漏气,现接通电源,电热丝对缸内气体缓慢加热.关于气缸内气体,下列说法正确的是
 (选修模块3-3)
(选修模块3-3) 如图所示,一气缸竖直放置,用一质量为m的活塞在缸内封闭了一定量的理想气体,在气缸的底部安装有一根电热丝,用导线和外界电源相连,已知气缸壁和活塞都是绝热的,气缸壁与活塞间接触光滑且不漏气.现接通电源,电热丝对缸内气体缓慢加热.
如图所示,一气缸竖直放置,用一质量为m的活塞在缸内封闭了一定量的理想气体,在气缸的底部安装有一根电热丝,用导线和外界电源相连,已知气缸壁和活塞都是绝热的,气缸壁与活塞间接触光滑且不漏气.现接通电源,电热丝对缸内气体缓慢加热.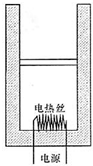 如图所示,一汽缸竖直放置,用一质量为m的活塞在缸内封闭了一定量的理想气体,在气缸的底部安装有一根电热丝,用导线和外界电源相连,已知气缸壁和活塞都是绝热的,气缸壁与活塞间接触光滑且不漏气,现接通电源,电热丝对缸内气体缓慢加热.关于气缸内气体,大列说法正确的是( )
如图所示,一汽缸竖直放置,用一质量为m的活塞在缸内封闭了一定量的理想气体,在气缸的底部安装有一根电热丝,用导线和外界电源相连,已知气缸壁和活塞都是绝热的,气缸壁与活塞间接触光滑且不漏气,现接通电源,电热丝对缸内气体缓慢加热.关于气缸内气体,大列说法正确的是( )