题目内容
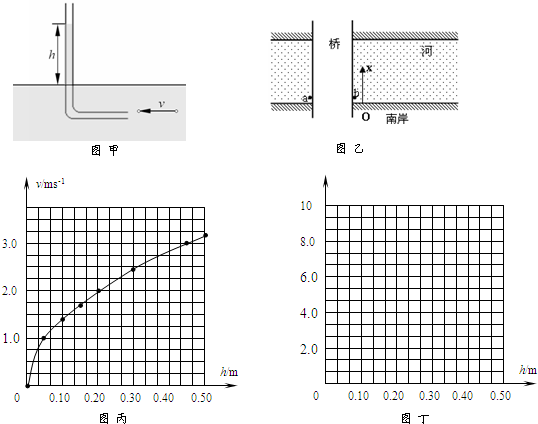
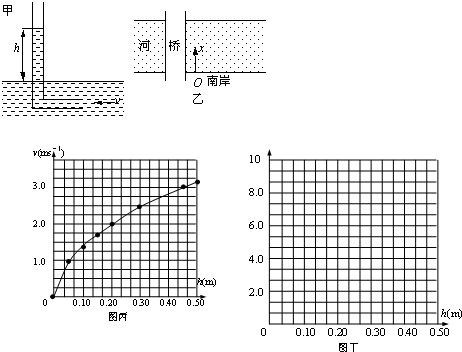
 如图为某同学设计的速度选择装置,两根足够长的光滑导轨MM′和NN′间距为L与水平面成θ角,上端接滑动变阻器R,匀强磁场B0垂直导轨平面向上,金属棒ab质量为m恰好垂直横跨在导轨上.滑动变阻器R两端连接水平放置的平行金属板,极板间距为d,板长为2d,匀强磁场B垂直纸面向内.粒子源能发射沿水平方向不同速率的带电粒子,粒子的质量为m0,电荷量为q,ab棒的电阻为r,滑动变阻器的最大阻值为2r,其余部分电阻不计,不计粒子重力.
如图为某同学设计的速度选择装置,两根足够长的光滑导轨MM′和NN′间距为L与水平面成θ角,上端接滑动变阻器R,匀强磁场B0垂直导轨平面向上,金属棒ab质量为m恰好垂直横跨在导轨上.滑动变阻器R两端连接水平放置的平行金属板,极板间距为d,板长为2d,匀强磁场B垂直纸面向内.粒子源能发射沿水平方向不同速率的带电粒子,粒子的质量为m0,电荷量为q,ab棒的电阻为r,滑动变阻器的最大阻值为2r,其余部分电阻不计,不计粒子重力.(1)ab棒静止未释放时,某种粒子恰好打在上极板中点P上,判断该粒子带何种电荷?该粒子的速度多大?
(2)调节变阻器使R=0.5r,然后释放ab棒,求ab棒的最大速度?
(3)当ab棒释放后达到最大速度时,若变阻器在r≤R≤2r范围调节,总有粒子能匀速穿过平行金属板,求这些粒子的速度范围?
分析:(1)粒子恰好打在上极板中点P上,由左手定则判断可知粒子带正电,根据几何知识求出粒子做圆周运动的半径,由牛顿第二定律求出粒子的速度.
(2)ab棒先向下做加速度减小的变加速运动,后做匀速运动,根据平衡条件和安培力公式求出最大速度.
(3)粒子能匀速穿过平行金属板,电场力与洛伦兹力平衡,则由平衡条件可求出电容器板间电压.由欧姆定律求出板间电压,联立即可求出这些粒子的速度范围.
(2)ab棒先向下做加速度减小的变加速运动,后做匀速运动,根据平衡条件和安培力公式求出最大速度.
(3)粒子能匀速穿过平行金属板,电场力与洛伦兹力平衡,则由平衡条件可求出电容器板间电压.由欧姆定律求出板间电压,联立即可求出这些粒子的速度范围.
解答:解:(1)由左手定则可知:该粒子带正电荷.
粒子在磁场中做圆周运动,设半径为r,速度为v0
由几何关系有:r2=d2+(r-
)2 ①
得:r=
d
粒子做匀速圆周运动,由牛顿第二定律得:Bqv0=
②
得:v0=
(2)ab棒达到最大速度时做匀速运动:mgsinθ=B0IL ③
对回路,由闭合电路欧姆定律:I=
④
由上得:v=
(3)当ab棒达到最大速度时,设变阻器接入电路电阻为R,电压为U
由③式得:I=
…④
对变阻器,由欧姆定律:U=IR ⑤
极板电压也为U,粒子匀速运动:Bqv1=
q ⑥
由④⑤⑥得:v1=
因为r≤R≤2r,故粒子的速度范围为:
≤v1≤
答:
(1)ab棒静止未释放时,某种粒子恰好打在上极板中点P上,该粒子带正电荷,该粒子的速度是
.
(2)ab棒的最大速度是
.
(3)这些粒子的速度范围为:
≤v1≤
粒子在磁场中做圆周运动,设半径为r,速度为v0
由几何关系有:r2=d2+(r-
| d |
| 2 |
得:r=
| 5 |
| 4 |
粒子做匀速圆周运动,由牛顿第二定律得:Bqv0=
m0
| ||
| r |
得:v0=
| 5Bqd |
| 4m0 |
(2)ab棒达到最大速度时做匀速运动:mgsinθ=B0IL ③
对回路,由闭合电路欧姆定律:I=
| B0Lv |
| 0.5r+r |
由上得:v=
| 3mgrsinθ | ||
2
|
(3)当ab棒达到最大速度时,设变阻器接入电路电阻为R,电压为U
由③式得:I=
| mgsinθ |
| B0L |
对变阻器,由欧姆定律:U=IR ⑤
极板电压也为U,粒子匀速运动:Bqv1=
| U |
| d |
由④⑤⑥得:v1=
| mgRsinθ |
| BB0Ld |
因为r≤R≤2r,故粒子的速度范围为:
| mgrsinθ |
| BB0Ld |
| 2mgrsinθ |
| BB0Ld |
答:
(1)ab棒静止未释放时,某种粒子恰好打在上极板中点P上,该粒子带正电荷,该粒子的速度是
| 5Bqd |
| 4m0 |
(2)ab棒的最大速度是
| 3mgrsinθ | ||
2
|
(3)这些粒子的速度范围为:
| mgrsinθ |
| BB0Ld |
| 2mgrsinθ |
| BB0Ld |
点评:本题是导体在导轨上滑动与速度选择器的组合,运用电磁感应、磁场、电路等多种知识进行分析研究,综合性较强.

练习册系列答案
相关题目