题目内容
【题目】如图,用一根长为L=1m的细线,一端系一质量为m=1kg的小球(可视为质点),另一端固定在一光滑锥体顶端,锥面与竖直方向的夹角θ=370,当小球在水平面内绕锥体的轴做匀速圆周运动的角速度为ω时,细线的张力为T.求
, 
, 
计算结果可用根式表示):
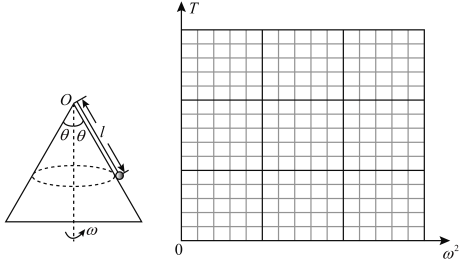
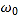
(1)若要小球离开锥面,则小球的角速度
至少为多大?
(2)若细线与竖直方向的夹角为600,则小球的角速度ω1为多大?
(3)细线的张力T与小球匀速转动的角速度ω有关,当ω的取值范围在0到ω1之间时,请通过计算求解T与ω2的关系,并在图坐标纸上作出T-ω2的图象,标明关键点的坐标值.
【答案】（1）
（2）
(3)见解析
【解析】（1）小球刚要离开锥面时的速度，此时支持力为零，根据牛顿第二定律得：
mgtanθ=mω02Lsin θ
解得： 
．
（2）同理，当细线与竖直方向成60°角时，由牛顿第二定律及向心力公式有：
mgtan α=mω′2Lsin α
解得： 
．
（3）a．当ω1=0时 T1=mgcosθ=8N，标出第一个特殊点坐标（ 0，8N）；
b．当0＜ω＜
rad/s时，根据牛顿第二定律得：
Tsinθ-Ncosθ=mω2Lsinθ，
Tcosθ+Nsinθ=mg
解得T＝mgcosθ+mLω2(sinθ)2＝8+
ω2
当ω2＝
rad/s时，T2=12.5N 标出第二个特殊点坐标[12.5（rad/s）2，12.5N]；
c．当
rad/s≤ω≤2
rad/s时，小球离开锥面，设细线与竖直方向夹角为β，
T3sinβ＝mω2Lsinβ
解得：T3＝mLω2
当ω＝ω′＝2
rad/s时，T3=20N
标出第三个特殊点坐标[20（rad/s）2，20N]．
画出T-ω2图象如图所示．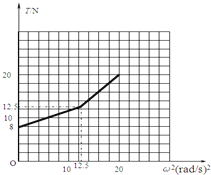
练习册系列答案
相关题目
