题目内容
1. 如图,在边长为L的等边三角形ABC区域内,存在垂直于所在平面向里的匀强磁场.大量的质量为m、电荷量为q的带正电粒子以相同速度(速度大小未确定)沿垂直于BC的方向射入磁场,经磁场偏转后三条边均有粒子射出,其中垂直于AB边射出的粒子在磁场中运动的时间为t0.不计粒子的重力及粒子间的相互作用.求:
如图,在边长为L的等边三角形ABC区域内,存在垂直于所在平面向里的匀强磁场.大量的质量为m、电荷量为q的带正电粒子以相同速度(速度大小未确定)沿垂直于BC的方向射入磁场,经磁场偏转后三条边均有粒子射出,其中垂直于AB边射出的粒子在磁场中运动的时间为t0.不计粒子的重力及粒子间的相互作用.求:(1)磁场的磁感应强度大小;
(2)要确保粒子能从BC边射出,射入的最大速度;
(3)AC、AB边上可能有粒子射出的范围.
分析 (1)根据几何关系求出粒子垂直AD射出时圆心角的大小,结合周期公式和运动的时间求出磁感应强度的大小.
(2)当轨迹圆与AC、AD都相切时,粒子能从CD边射出,半径最大,速度为最大值,根据几何关系求出半径,结合半径公式求出最大速度.
(3)当轨迹圆与AC相切时,从AC边射出的粒子距C最远,当轨迹圆与AD边的交点F恰在圆心O正上方时,射出的粒子距D点最远,结合几何 关系求出AC、AD边上可能有粒子射出的范围.
解答 解:(1)垂直于AB边射出的粒子轨迹对应圆心角为600,则:t0=$\frac{1}{6}$T,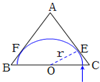
据牛顿第二定律得:qvB=m$\frac{{v}^{2}}{r}$,
解得:r=$\frac{mv}{qB}$,T=$\frac{2πm}{qB}$,
解得:B=$\frac{πm}{3q{t}_{0}}$;
(2)当粒子轨迹圆与AB、AC都相切时,能从BC边射出的粒子的半径最大,
对应速度为最大值,此时:r=$\frac{L}{2}$sin60°=$\frac{\sqrt{3}}{4}$L,解得:vmax=$\frac{\sqrt{3}πL}{12{t}_{0}}$; (3)由(2)知,当轨迹圆与AC相切时,从AC边射出的粒子距C最远,
(3)由(2)知,当轨迹圆与AC相切时,从AC边射出的粒子距C最远,
故有粒子射出的范围为CE段,CE=$\frac{L}{2}$cos60°=$\frac{L}{4}$,
当轨迹圆与AD边的交点D恰在圆心O正上方时,射出的粒子距B点最远.
故有粒子射出的范围为BD段,BD=$\frac{r}{sin60°}$=$\frac{1}{2}$L;
答:(1)磁场的磁感应强度大小为$\frac{πm}{3q{t}_{0}}$;
(2)要确保粒子能从BC边射出,射入的最大速度为$\frac{\sqrt{3}πL}{12{t}_{0}}$;
(3)AC、AB边上可能有粒子射出的范围:$\frac{1}{4}$L≤x≤$\frac{1}{2}$L.
点评 本题考查了带电粒子在磁场中的运动,关键作出运动的轨迹,抓住临界状态,结合半径公式和周期公式进行求解,难度中等.

 阅读快车系列答案
阅读快车系列答案 如图所示,斜面体C置于水平地面上,小物块B置于斜面上,通过细绳跨过光滑的定滑轮与沙漏A连接,连接B的一段细绳与斜面平行.在A中的沙子缓慢流出的过程中,A、B、C都处于静止状态,则在此过程中( )
如图所示,斜面体C置于水平地面上,小物块B置于斜面上,通过细绳跨过光滑的定滑轮与沙漏A连接,连接B的一段细绳与斜面平行.在A中的沙子缓慢流出的过程中,A、B、C都处于静止状态,则在此过程中( )| A. | B对C的摩擦力大小一定减小 | |
| B. | C对B的作用力大小可能先减小后增大 | |
| C. | 地面对C的摩擦力大小可能不变 | |
| D. | C对地面的摩擦力方向始终水平向左 |
| A. | 在验证力的平行四边形定则的实验中使用了控制变量的方法 | |
| B. | 在探究加速度、力和质童三者之间的关系时,先保持质量不变研究加速度与力的关系,再保持力不变研究加速度与质量的关系,该实验采用了假设法 | |
| C. | 在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段都近似看作匀速直线运动,然后把各小段的位移相加,这里采用了理想模型法 | |
| D. | 根据平均速度定义式:$\overline{v}$=$\frac{△x}{△t}$,当△t非常小时,$\frac{△x}{△t}$就可以表示物体在t时刻的瞬时速度,该定义运用了极限思想方法 |
| A. | 大于7.9 km/s | B. | 介于7.9 km/s~11.2 km/s之间 | ||
| C. | 小于或等于7.9 km/s | D. | 一定大于11.2 km/s |
表1 物体质量一定时,加速度与力的关系
| a/(m/s2) | 0.20 | 0.40 | 0.61 | 0.79 | 0.97 |
| F/N | 0.14 | 0.28 | 0.43 | 0.55 | 0.68 |
| a/(m/s2) | 1.08 | 0.89 | 0.73 | 0.56 | 0.44 |
| m/kg | 0.20 | 0.25 | 0.30 | 0.40 | 0.50 |

由该图象得出的结论是:a与F成正比.
(2)根据表2数据在图2中作出a-m图象
由该图象得出的结论是:a随着m增大而减小.
 如图,匀强电场水平向右,虚线为一带电粒子在匀强电场中从A点运动到B点的轨迹,此过程粒子克服重力做功为5J,静电力做功为3J,则下列说法中国正确的是( )
如图,匀强电场水平向右,虚线为一带电粒子在匀强电场中从A点运动到B点的轨迹,此过程粒子克服重力做功为5J,静电力做功为3J,则下列说法中国正确的是( )| A. | 粒子带负电 | B. | 粒子在A点的动能比在B点少2J | ||
| C. | 粒子在A点的电势能比在B点少3J | D. | 粒子在A点的机械能比在B点少3J |
 法拉第发明了世界上第一台发电机-法拉第圆盘发电机.如图所示,圆形铜盘水平放置在竖直向下的匀强磁场中,圆盘圆心处固定一个摇柄,边缘和圆心处各有一个黄铜电刷紧贴,用导线将电刷与电流表连接起来形成回路.转动摇柄,使圆盘逆时针匀速转动,电流计的指针发生偏转,则回路中( )
法拉第发明了世界上第一台发电机-法拉第圆盘发电机.如图所示,圆形铜盘水平放置在竖直向下的匀强磁场中,圆盘圆心处固定一个摇柄,边缘和圆心处各有一个黄铜电刷紧贴,用导线将电刷与电流表连接起来形成回路.转动摇柄,使圆盘逆时针匀速转动,电流计的指针发生偏转,则回路中( )| A. | 电流大小变化,方向不变 | |
| B. | 电流大小不变,方向变化 | |
| C. | 电流大小和方向都发生周期性变化 | |
| D. | 电流的大小、方向都不变,电流从b导线流进电流表 |
 如图所示,其中v=2m/s,木块质量m=10kg,h=2m,μ=$\frac{\sqrt{3}}{2}$,θ=30°,g取10m/s2.
如图所示,其中v=2m/s,木块质量m=10kg,h=2m,μ=$\frac{\sqrt{3}}{2}$,θ=30°,g取10m/s2. 如图所示,匀强磁场的磁感应强度为B,方向垂直纸面向里.匀强磁场中有一折成θ角的金属导轨aOb,导轨平而垂直磁场方向.一条直导线MN垂直Ob方向放置在导轨上并接触良好,MN受水平拉力F以初速v从导轨O点开始向右沿水平方向匀速运动,若导轨和直导线的单位长度的电阻都为r,设闭合回路的感应电流大小为I,则下列的I-t、F-t图象正确的是( )
如图所示,匀强磁场的磁感应强度为B,方向垂直纸面向里.匀强磁场中有一折成θ角的金属导轨aOb,导轨平而垂直磁场方向.一条直导线MN垂直Ob方向放置在导轨上并接触良好,MN受水平拉力F以初速v从导轨O点开始向右沿水平方向匀速运动,若导轨和直导线的单位长度的电阻都为r,设闭合回路的感应电流大小为I,则下列的I-t、F-t图象正确的是( )