题目内容
19. 如图所示,其中v=2m/s,木块质量m=10kg,h=2m,μ=$\frac{\sqrt{3}}{2}$,θ=30°,g取10m/s2.
如图所示,其中v=2m/s,木块质量m=10kg,h=2m,μ=$\frac{\sqrt{3}}{2}$,θ=30°,g取10m/s2.(1)求小木块从A端由静止运动到B端,传送带对其做的功是多少?
(2)摩擦产生的热为多少?
(3)因传送小木块电动机多输出的能量.
分析 (1)由牛顿第二定律可求得物体运动的加速度,而物体和传送带速度相等时二者相对静止,由位移公式可求得物体加速上滑的位移,则恒力做功公式即可求得此过程中摩擦力对物体所做的功,此后做匀速运动,再求出摩擦力做功;
(2)摩擦产生的内能等于摩擦力乘以相对位移;
(3)由功能关系可求得电动机多消耗的能量.
解答 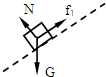 解:(1)木块先匀加速运动,受力如图,则有
解:(1)木块先匀加速运动,受力如图,则有
N=mgcosθ,f1-mgsinθ=ma,滑动摩擦力:f1=μN.
代入数据解得:a=2.5m/s2,
此过程的上滑位移x1=$\frac{{v}^{2}}{2a}$=0.8m,
运动的时间t1=$\frac{v}{a}$=0.8s,
此过程中摩擦力做功:W1=f1x1=60J,
接着木块匀速运动,f2=mgsinθ=100×0.5=50N
W2=f2x2=50×3.2=160J,
则传送带对木块做功为W=W1+W2=60+160=220J
(2)第一阶段摩擦生热:
Q=f1x相对=f1(vt1-x1)=75×0.8=60J
(3)由功能关系知△E电=W+Q=220+60=280J
答:
(1)小木块从A端由静止运动到B端,传送带对其做的功是220J.
(2)摩擦产生的热为60J;
(3)因传送小木块电动机多输出的能量为280J.
点评 本题为传送带问题,要注意分析物体在传送带上的受力情况及运动情况,综合利用牛顿第二定律及动能定理、功能关系等方法求解.

练习册系列答案
相关题目
9.甲、乙两物体由同一位置出发沿同一直线运动时的v-t图象如图所示,则( )


| A. | 甲作匀速直线运动 | |
| B. | 乙在2秒内作匀加速直线运动,2秒后作匀减速直线运动 | |
| C. | 两物体两次相遇时刻是1秒末和4秒末 | |
| D. | 甲、乙两物体的速度方向相反 |
10. 如图所示,高为h=1.25m的平台上,覆盖一层薄冰,现有一质量为60kg的滑雪爱好者,以一定的初速度v向平台边缘滑去,着地时的速度方向与水平地面的夹角为45°(取重力加速度g=10m/s2).由此可知下列各项中错误的是( )
如图所示,高为h=1.25m的平台上,覆盖一层薄冰,现有一质量为60kg的滑雪爱好者,以一定的初速度v向平台边缘滑去,着地时的速度方向与水平地面的夹角为45°(取重力加速度g=10m/s2).由此可知下列各项中错误的是( )
 如图所示,高为h=1.25m的平台上,覆盖一层薄冰,现有一质量为60kg的滑雪爱好者,以一定的初速度v向平台边缘滑去,着地时的速度方向与水平地面的夹角为45°(取重力加速度g=10m/s2).由此可知下列各项中错误的是( )
如图所示,高为h=1.25m的平台上,覆盖一层薄冰,现有一质量为60kg的滑雪爱好者,以一定的初速度v向平台边缘滑去,着地时的速度方向与水平地面的夹角为45°(取重力加速度g=10m/s2).由此可知下列各项中错误的是( )| A. | 滑雪者离开平台边缘时的速度大小是5.0m/s | |
| B. | 滑雪者着地点到平台边缘的水平距离是2.5m | |
| C. | 滑雪者在空中运动的时间为1s | |
| D. | 着地时滑雪者重力做功的瞬时功率是300W |
14.一质量为m,电量为q的微观粒子沿垂直场强方向从中央射入两平行带电板之间,当粒子的入射速度为v0时,恰好能穿越平行板电场,为使其入射速度减半时仍恰能穿越电场,则必须使得( )
| A. | 粒子的电量减半 | B. | 两板间电压减半 | C. | 两板间距加倍 | D. | 两板间距减半 |
4.下列哪些现象属于能量的耗散( )
| A. | 利用水流能发电产生电能 | B. | 电能在灯泡中变成光能 | ||
| C. | 电池的化学能变成电能 | D. | 火炉把屋子烤暖 |
2.关于开普勒行星运动的公式$\frac{{R}^{3}}{{T}^{2}}$=K,以下理解不正确的是( )
| A. | K是一个与行星有关的常数 | B. | K是一个与恒星有关的常数 | ||
| C. | T表示行星运动的公转周期 | D. | R表示轨道的半长轴 |
 如图所示,质量为m1=2kg的物体甲通过三段轻绳悬挂,三段轻绳的结点为O,轻绳OB水平且B端与放置在水平面上的质量为m2的物体乙相连,轻绳OA与竖直方向的夹角θ=37°,物体甲、乙均处于静止状态.已知重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.设最大静摩擦力等于滑动摩擦力,求:
如图所示,质量为m1=2kg的物体甲通过三段轻绳悬挂,三段轻绳的结点为O,轻绳OB水平且B端与放置在水平面上的质量为m2的物体乙相连,轻绳OA与竖直方向的夹角θ=37°,物体甲、乙均处于静止状态.已知重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.设最大静摩擦力等于滑动摩擦力,求: 如图,在边长为L的等边三角形ABC区域内,存在垂直于所在平面向里的匀强磁场.大量的质量为m、电荷量为q的带正电粒子以相同速度(速度大小未确定)沿垂直于BC的方向射入磁场,经磁场偏转后三条边均有粒子射出,其中垂直于AB边射出的粒子在磁场中运动的时间为t0.不计粒子的重力及粒子间的相互作用.求:
如图,在边长为L的等边三角形ABC区域内,存在垂直于所在平面向里的匀强磁场.大量的质量为m、电荷量为q的带正电粒子以相同速度(速度大小未确定)沿垂直于BC的方向射入磁场,经磁场偏转后三条边均有粒子射出,其中垂直于AB边射出的粒子在磁场中运动的时间为t0.不计粒子的重力及粒子间的相互作用.求: