Question

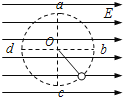
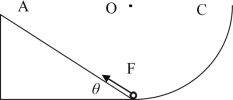
【题目】如图，在同一竖直面内，有足够长的粗糙直轨道AB，与水平方向的夹角θ＝37°；光滑圆轨道BC半径R=40m，圆心O点位于B点正上方，两个轨道在B处平滑连接。一质量m＝2kg的小球一开始静止在B点，现给小球一个平行于AB向上的恒定拉力F，在经过t1＝0.4s后撤去拉力F，小球沿AB轨道上升的最大高度h=0.15m。已知小球与AB间动摩擦因数μ＝0.5。不计小球经过B点时的机械能损失。（sin37°＝0.6，cos37°＝0.8，cos5°=0.996）求：

(1)撤去拉力F后小球在斜面上运动的加速度大小；

(2)恒定拉力F的大小；

(3)从出发到小球第二次回到B点的总时间t。

Answer 1

【答案】(1)；；(2)；(3)

【解析】

(1)小球在斜面上先加速再减速，之后沿斜面向下运动。设撤去拉力F后小球在斜面上向上运动的加速度大小为a2，向下运动的加速度大小为a3，则

解得

(2)小球在斜面上向上运动过程有

解得

所以

根据牛顿第二定律有

解得

(3)小球在斜面上向上减速过程有

小球第一次回到B点有

则

设小球在圆轨道上升的最大高度H，则

解得

小球在圆轨道上做简谐运动，有

所以