Question

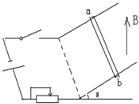
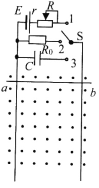
【题目】如图所示，竖直放置的两根足够长的光滑金属导轨相距L，导轨的两端分别与电源（串有一滑动变阻器R）、定值电阻R0、电容器（电容为C，原来不带电）和开关S相连。整个空间充满了磁感应强度大小为B、方向垂直于导轨平面向外的匀强磁场。一质量为m、电阻不计的金属棒横跨在导轨上。己知电源电动势为E、内阻为r，不计导轨的电阻。当S接1，滑动变阻器R接入电路一定阻值时，金属棒ab在磁场中恰好保持静止。当S接2后，金属棒ab从静止开始下落，下落距离时达到稳定速度。重力加速度为g，则下列分析正确的是（　　）

A.当S接1时，滑动变阻器接入电路的阻值

B.当S接2时，金属棒从静止开始到刚好达到稳定速度所经历的时间为

C.若将棒由静止释放的同时，将S接到3，则电容器积累的电荷量随金属棒速度v的变化关系为

D.若将棒由静止释放的同时，将S接到3，则金属棒将做匀加速直线运动，加速度大小

Answer 1

【答案】ACD

【解析】

A．S接到1位置时，有

由平衡条件得

mg=BIL

得

联立解得

故A正确；
B．S接到2位置速度恒定时有

解得

金属棒ab从静止开始下落，下落距离h时达到稳定速度，根据动量定理可得

即

其中，解得

故B错误；
CD．若将ab棒由静止释放的同时，将S接到3，则电容器积累的电荷量随金属棒速度v的变化关系为

Q=CU=CBLv

根据动量定理可得

即

mg△t-BL△Q=m△v

将△Q=CBL△v代入解得

mg△t-CB2L2△v=m△v

所以

故CD正确。
故选ACD。