题目内容
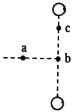
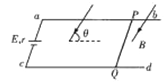
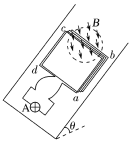
【题目】如图所示,粗糙斜面的倾角θ=37°,半径r=0.5 m的圆形区域内存在着垂直于斜面向下的匀强磁场.一个匝数n=10匝的刚性正方形线框abcd,通过松弛的柔软导线与一个额定功率P=1.25 W的小灯泡A相连,圆形磁场的一条直径恰好过线框bc边.已知线框质量m=2 kg,总电阻R0=1.25 Ω,边长L>2r,与斜面间的动摩擦因数μ=0.5.从t=0时起,磁场的磁感应强度按B=2-![]() t(T)的规律变化.开始时线框静止在斜面上,在线框运动前,灯泡始终正常发光.设最大静摩擦力等于滑动摩擦力,g取10 m/s2,sin 37°=0.6,cos 37°=0.8.求:
t(T)的规律变化.开始时线框静止在斜面上,在线框运动前,灯泡始终正常发光.设最大静摩擦力等于滑动摩擦力,g取10 m/s2,sin 37°=0.6,cos 37°=0.8.求:
(1)小灯泡正常发光时的电阻R;
(2)线框保持不动的时间内,小灯泡产生的热量Q.
【答案】(1)1.25 Ω (2)3.14 J
【解析】
(1)根据法拉第电磁感应定律,即可求解感应电动势;由功率表达式,结合闭合电路欧姆定律即可;
(2)对线框受力分析,并结合平衡条件,及焦耳定律,从而求得。
(1)由法拉第电磁感应定律有E=n![]()
得![]()
小灯泡正常发光,有P=I2R
由闭合电路欧姆定律有E=I(R0+R)
则有P=(![]() )2R,代入数据解得R=1.25 Ω.
)2R,代入数据解得R=1.25 Ω.
(2)对线框受力分析如图
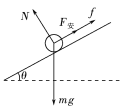
设线框恰好要运动时,磁场的磁感应强度大小为B′,由力的平衡条件有
mgsin θ=F安+f=F安+μmgcos θ
F安=nB′I×2r
联立解得线框刚要运动时,磁场的磁感应强度大小B′=0.4 T
线框在斜面上可保持静止的时间![]()
小灯泡产生的热量Q=Pt=1.25×![]() J=3.14 J.
J=3.14 J.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目