题目内容
18. 如图,一端接有定值电阻R的足够长的平行金属导轨,放在绝缘斜面上(斜面未画出),匀强磁场垂直于导轨平面向上,导体棒ab垂直于导轨放置.现给导体棒沿斜面向上的初速度v,经过一段时间导体棒又回到原位置.在运动过程中导体棒ab始终垂直于导轨,导轨和导体棒的电阻可忽略不计.则( )
如图,一端接有定值电阻R的足够长的平行金属导轨,放在绝缘斜面上(斜面未画出),匀强磁场垂直于导轨平面向上,导体棒ab垂直于导轨放置.现给导体棒沿斜面向上的初速度v,经过一段时间导体棒又回到原位置.在运动过程中导体棒ab始终垂直于导轨,导轨和导体棒的电阻可忽略不计.则( )| A. | 在上滑过程导体棒中的电流方向由a到b | |
| B. | 回到原位置时导体棒的速度大小仍为v | |
| C. | 开始上滑和回到原位置时导体棒的加速度大小相等 | |
| D. | 上滑过程与下滑到初始位置的过程通过导体棒截面的电荷量相等 |
分析 根据右手定则判断感应电流的方向;根据能量守恒定律分析金属棒回到原位置的速度大小;根据安培力与速度的关系及牛顿第二定律分析加速度的大小关系;根据公式q=$\frac{△Φ}{R}$分析通过棒的电量关系.
解答 解:
A、金属棒上滑时,根据右手定则判断可知棒中感应电流的方向由b到a,故A错误.
B、金属棒运动过程中产生感应电流,受到安培力作用,根据楞次定律可知安培力总是阻碍金属棒相对于导轨运动,所以金属棒的机械能不断减小,则金属棒回到原位置是速度大小必小于v.故B错误.
C、根据牛顿第二定律得:
对于上滑过程:mgsinθ+F安=ma上;对于下滑过程:mgsinθ-F安′=ma下;可知:a上>a下.故C错误.
D、金属棒上滑阶段和下滑阶段中回路磁通量的变化量相等,根据q=$\frac{△Φ}{R}$可知通过棒的电量相等,故D正确.
故选:D.
点评 解决本题的关键通过能量守恒定律比较出回到出发点的速度和初速度的大小,从而确定每个位置感应电流和速度的大小.记住感应电量经验公式q=$\frac{△Φ}{R}$,研究电量问题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
13. 如图所示,平行板电容器A、B板与电源正、负极相连,B板接地,电容器中有一固定点P.闭合电键K,给电容器充电,然后断开K.下列说法正确的是( )
如图所示,平行板电容器A、B板与电源正、负极相连,B板接地,电容器中有一固定点P.闭合电键K,给电容器充电,然后断开K.下列说法正确的是( )
 如图所示,平行板电容器A、B板与电源正、负极相连,B板接地,电容器中有一固定点P.闭合电键K,给电容器充电,然后断开K.下列说法正确的是( )
如图所示,平行板电容器A、B板与电源正、负极相连,B板接地,电容器中有一固定点P.闭合电键K,给电容器充电,然后断开K.下列说法正确的是( )| A. | 只向下平移A板,P点电场强度增大,P点电势升高 | |
| B. | 只向下平移A板,P点电场强度不变,P点电势不变 | |
| C. | 只向左平移B板,P点电场强度变大,P点电势升高 | |
| D. | 只向右平移B板,P点电场强度变小,P点电势降低 |
3. 如图所示,两个固定的光滑半圆碗,半径分别为R1,R2且R1>R2,质量相等的A、B两小球,从碗的上边缘由静止滚下,碗的上边缘,在同一水平面上,设为零势位.下述正确的是( )
如图所示,两个固定的光滑半圆碗,半径分别为R1,R2且R1>R2,质量相等的A、B两小球,从碗的上边缘由静止滚下,碗的上边缘,在同一水平面上,设为零势位.下述正确的是( )
 如图所示,两个固定的光滑半圆碗,半径分别为R1,R2且R1>R2,质量相等的A、B两小球,从碗的上边缘由静止滚下,碗的上边缘,在同一水平面上,设为零势位.下述正确的是( )
如图所示,两个固定的光滑半圆碗,半径分别为R1,R2且R1>R2,质量相等的A、B两小球,从碗的上边缘由静止滚下,碗的上边缘,在同一水平面上,设为零势位.下述正确的是( )| A. | 小球由静止滚下,在达最低点P过程中,小球受到的合外力总是指向圆心 | |
| B. | 两小球达到最低点P时,对碗的压力相同 | |
| C. | 两小球在最低点P时,机械能相等 | |
| D. | 两小球达最低点P时速度相同 |
10.质量为m 的物体以初速度v0从地面竖直上抛,不计空气阻力,当它抛到离地面h高处时,它的动能恰好为重力势能的3倍(地面为重力势能参考面),则这个高度为h为( )
| A. | $\frac{v_0^2}{4g}$ | B. | $\frac{3v_0^2}{4g}$ | C. | $\frac{3v_0^2}{8g}$ | D. | $\frac{v_0^2}{8g}$ |
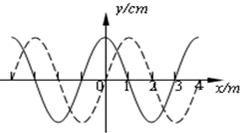 一列简谐横波,如图中的实线是某时刻的波形图象,虚线是经过0.2s时的波形图象
一列简谐横波,如图中的实线是某时刻的波形图象,虚线是经过0.2s时的波形图象