题目内容
8.某行星的半径是地球半径的2倍,密度与地球的密度相等,已知地球的第一宇宙速度为7.9km/s,则该行星的第一宇宙速度是15.8km/s.分析 第一宇宙速度等于卫星绕行星附近做匀速圆周运动的速度,卫星的向心力由行星的万有引力提供,结合密度公式,列式求解.
解答 解:设行星的第一宇宙速度为v1,质量为M,半径为R,地球的第一宇宙速度为v1,地球质量为M0,半径为R0.卫星的质量为m.
则根据万有引力等于向心力,得:
G$\frac{Mm}{{R}^{2}}$=m$\frac{{v}^{2}}{R}$,
解得:v1=$\sqrt{\frac{GM}{R}}$;
同理得,v2=$\sqrt{\frac{G{M}_{0}}{{R}_{0}}}$.
又M=ρ•$\frac{4}{3}$πR3,
M0=ρ•$\frac{4}{3}$πR03.
联立上四式得:$\frac{{v}_{1}}{{v}_{2}}$=$\frac{R}{{R}_{0}}$=$\frac{2}{1}$,
得:v1=2v2=2×7.9km/s=15.8km/s
故答案为:15.8km/s.
点评 本题首先要理解并掌握第一宇宙速度的定义,其次掌握卫星问题常用的思路:万有引力等于向心力.

练习册系列答案
相关题目
18. 如图,一端接有定值电阻R的足够长的平行金属导轨,放在绝缘斜面上(斜面未画出),匀强磁场垂直于导轨平面向上,导体棒ab垂直于导轨放置.现给导体棒沿斜面向上的初速度v,经过一段时间导体棒又回到原位置.在运动过程中导体棒ab始终垂直于导轨,导轨和导体棒的电阻可忽略不计.则( )
如图,一端接有定值电阻R的足够长的平行金属导轨,放在绝缘斜面上(斜面未画出),匀强磁场垂直于导轨平面向上,导体棒ab垂直于导轨放置.现给导体棒沿斜面向上的初速度v,经过一段时间导体棒又回到原位置.在运动过程中导体棒ab始终垂直于导轨,导轨和导体棒的电阻可忽略不计.则( )
 如图,一端接有定值电阻R的足够长的平行金属导轨,放在绝缘斜面上(斜面未画出),匀强磁场垂直于导轨平面向上,导体棒ab垂直于导轨放置.现给导体棒沿斜面向上的初速度v,经过一段时间导体棒又回到原位置.在运动过程中导体棒ab始终垂直于导轨,导轨和导体棒的电阻可忽略不计.则( )
如图,一端接有定值电阻R的足够长的平行金属导轨,放在绝缘斜面上(斜面未画出),匀强磁场垂直于导轨平面向上,导体棒ab垂直于导轨放置.现给导体棒沿斜面向上的初速度v,经过一段时间导体棒又回到原位置.在运动过程中导体棒ab始终垂直于导轨,导轨和导体棒的电阻可忽略不计.则( )| A. | 在上滑过程导体棒中的电流方向由a到b | |
| B. | 回到原位置时导体棒的速度大小仍为v | |
| C. | 开始上滑和回到原位置时导体棒的加速度大小相等 | |
| D. | 上滑过程与下滑到初始位置的过程通过导体棒截面的电荷量相等 |
19. 如图所示,半径相同的两个金属小球A、B带有电荷量大小相等的电荷(可视为点电荷),相隔一定的距离,两球之间的相互吸引力大小为F,今用第三个半径相同的不带电的金属小球C先后与A、B两个球接触后移开,这时,A、B两个球之间的相互作用力大小是( )
如图所示,半径相同的两个金属小球A、B带有电荷量大小相等的电荷(可视为点电荷),相隔一定的距离,两球之间的相互吸引力大小为F,今用第三个半径相同的不带电的金属小球C先后与A、B两个球接触后移开,这时,A、B两个球之间的相互作用力大小是( )
 如图所示,半径相同的两个金属小球A、B带有电荷量大小相等的电荷(可视为点电荷),相隔一定的距离,两球之间的相互吸引力大小为F,今用第三个半径相同的不带电的金属小球C先后与A、B两个球接触后移开,这时,A、B两个球之间的相互作用力大小是( )
如图所示,半径相同的两个金属小球A、B带有电荷量大小相等的电荷(可视为点电荷),相隔一定的距离,两球之间的相互吸引力大小为F,今用第三个半径相同的不带电的金属小球C先后与A、B两个球接触后移开,这时,A、B两个球之间的相互作用力大小是( )| A. | $\frac{F}{8}$ | B. | $\frac{F}{4}$ | C. | $\frac{3F}{8}$ | D. | $\frac{3F}{4}$ |
20.如图,一平面简谐波以波速u沿x轴正方形传播,O为坐标原点,已知P点的振动方程为y=Acosωt,则( )
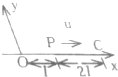

| A. | O点的振动方程为y=Acosω(t-$\frac{1}{u}$) | B. | 波的表达式为y=Acosω[t-($\frac{1}{u}$)-($\frac{x}{u}$)] | ||
| C. | 波的表达式为y=Acosω[t+($\frac{1}{u}$)-($\frac{x}{u}$)] | D. | C点的振动方程为y=Acosω(t-$\frac{3l}{u}$) |
 “测定玻璃的折射率”实验中,下图是在纸上留下的实验痕迹,其中直线a、a′是描在纸上的玻璃砖的两个边.
“测定玻璃的折射率”实验中,下图是在纸上留下的实验痕迹,其中直线a、a′是描在纸上的玻璃砖的两个边.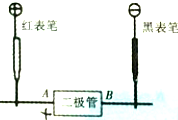 某同学利用多用电表的电阻档判断二极管的正负极,当红表笔接A端,黑表笔接B端时,电阻很小;当黑表笔接A端,红表笔接B端时,电阻很大,如图所示,则B(填“A”或“B”)端是二极管的正极.
某同学利用多用电表的电阻档判断二极管的正负极,当红表笔接A端,黑表笔接B端时,电阻很小;当黑表笔接A端,红表笔接B端时,电阻很大,如图所示,则B(填“A”或“B”)端是二极管的正极.