题目内容
7.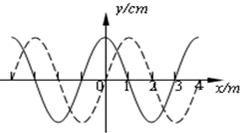 一列简谐横波,如图中的实线是某时刻的波形图象,虚线是经过0.2s时的波形图象
一列简谐横波,如图中的实线是某时刻的波形图象,虚线是经过0.2s时的波形图象(1)若这列波向右传播,求波速?
(2)假定波速是35m/s,若有一质点P、其平衡位置的坐标是x=0.5m,从实线对应的时刻开始计时,求经过多长时间可以到达平衡位置?
分析 (1)根据传播的时间,结合波传播的周期性求出周期的大小,根据波长和周期求出波速.
(2)根据波速的大小,结合周期的大小得出波传播的方向,进而求出到达平衡位置的时间.
解答 解:(1)由题意得,如果波向右传播,则所需时间t=nT+$\frac{T}{4}$=0.2s(n=0,1,2…)
v=$\frac{λ}{T}$=5(4n+1)m/s (n=0,1,2…)
(2)如果波向左传播,所需时间t=nT+$\frac{3T}{4}$=0.2s(n=0,1,2…),
那么T=$\frac{0.8}{4n+3}$s(n=0,1,2…),
v=$\frac{λ}{T}$=5(4n+3)m/s(n=0,1,2…),
如果v=35m/s,解得n=1,符合取值范围,所以波是向左传播
这时T=$\frac{4}{35}$s所需要的时间t=$\frac{0.5+2n}{4}T$=$\frac{0.5+2n}{35}$s (n=0,1,2…)
答:(1)波速为5(4n+1)m/s,(n=0,1,2…)
(2)经过$\frac{0.5+2n}{35}$s,(n=0,1,2…)可以到达平衡位置.
点评 本题考查理解波动图象的能力以及运用数学通项求解特殊值的能力.对于两个时刻的波形,有时还要考虑波的双向性.

练习册系列答案
相关题目
17. 如图,从地面上方某点,将一小球以10m/s的初速度沿水平方向抛出,小球经过1s落地,不计空气阻力,g=10m/s2,则可求出( )
如图,从地面上方某点,将一小球以10m/s的初速度沿水平方向抛出,小球经过1s落地,不计空气阻力,g=10m/s2,则可求出( )
 如图,从地面上方某点,将一小球以10m/s的初速度沿水平方向抛出,小球经过1s落地,不计空气阻力,g=10m/s2,则可求出( )
如图,从地面上方某点,将一小球以10m/s的初速度沿水平方向抛出,小球经过1s落地,不计空气阻力,g=10m/s2,则可求出( )| A. | 小球抛出时离地面的高度是5m | |
| B. | 小球从抛出点到落地点的位移大小是10m | |
| C. | 小球落地时的速度大小是20m/s | |
| D. | 小球落地时的速度方向与水平地面成60°角 |
18. 如图,一端接有定值电阻R的足够长的平行金属导轨,放在绝缘斜面上(斜面未画出),匀强磁场垂直于导轨平面向上,导体棒ab垂直于导轨放置.现给导体棒沿斜面向上的初速度v,经过一段时间导体棒又回到原位置.在运动过程中导体棒ab始终垂直于导轨,导轨和导体棒的电阻可忽略不计.则( )
如图,一端接有定值电阻R的足够长的平行金属导轨,放在绝缘斜面上(斜面未画出),匀强磁场垂直于导轨平面向上,导体棒ab垂直于导轨放置.现给导体棒沿斜面向上的初速度v,经过一段时间导体棒又回到原位置.在运动过程中导体棒ab始终垂直于导轨,导轨和导体棒的电阻可忽略不计.则( )
 如图,一端接有定值电阻R的足够长的平行金属导轨,放在绝缘斜面上(斜面未画出),匀强磁场垂直于导轨平面向上,导体棒ab垂直于导轨放置.现给导体棒沿斜面向上的初速度v,经过一段时间导体棒又回到原位置.在运动过程中导体棒ab始终垂直于导轨,导轨和导体棒的电阻可忽略不计.则( )
如图,一端接有定值电阻R的足够长的平行金属导轨,放在绝缘斜面上(斜面未画出),匀强磁场垂直于导轨平面向上,导体棒ab垂直于导轨放置.现给导体棒沿斜面向上的初速度v,经过一段时间导体棒又回到原位置.在运动过程中导体棒ab始终垂直于导轨,导轨和导体棒的电阻可忽略不计.则( )| A. | 在上滑过程导体棒中的电流方向由a到b | |
| B. | 回到原位置时导体棒的速度大小仍为v | |
| C. | 开始上滑和回到原位置时导体棒的加速度大小相等 | |
| D. | 上滑过程与下滑到初始位置的过程通过导体棒截面的电荷量相等 |
15. 如图所示,质量为M,长为L的车厢静止在光滑水平面上,此时质量为m的木块正以水平速度v从左边进入车厢板向右运动,车厢底板粗糙,m与右壁B发生无能量损失的碰撞后又被弹回,最后又恰好停在车厢左端点A,则以下叙述中正确的是( )
如图所示,质量为M,长为L的车厢静止在光滑水平面上,此时质量为m的木块正以水平速度v从左边进入车厢板向右运动,车厢底板粗糙,m与右壁B发生无能量损失的碰撞后又被弹回,最后又恰好停在车厢左端点A,则以下叙述中正确的是( )
 如图所示,质量为M,长为L的车厢静止在光滑水平面上,此时质量为m的木块正以水平速度v从左边进入车厢板向右运动,车厢底板粗糙,m与右壁B发生无能量损失的碰撞后又被弹回,最后又恰好停在车厢左端点A,则以下叙述中正确的是( )
如图所示,质量为M,长为L的车厢静止在光滑水平面上,此时质量为m的木块正以水平速度v从左边进入车厢板向右运动,车厢底板粗糙,m与右壁B发生无能量损失的碰撞后又被弹回,最后又恰好停在车厢左端点A,则以下叙述中正确的是( )| A. | 该过程中产生的内能为$\frac{1}{2}$mv2 | |
| B. | 车厢底板的动摩擦因数为$\frac{{M{v^2}}}{4(m+M)gL}$ | |
| C. | M的最终速度为$\frac{mv}{m+M}$ | |
| D. | m、M最终速度为零 |
12.质点做直线运动的位移s和时间平方t2的关系图象如图所示,该质点( )


| A. | 加速度大小为1 m/s2 | B. | 任意相邻1 s内的位移差都为2 m | ||
| C. | 第2 s内的位移是2 m | D. | 第3 s内的平均速度大小为3 m/s |
19. 如图所示,半径相同的两个金属小球A、B带有电荷量大小相等的电荷(可视为点电荷),相隔一定的距离,两球之间的相互吸引力大小为F,今用第三个半径相同的不带电的金属小球C先后与A、B两个球接触后移开,这时,A、B两个球之间的相互作用力大小是( )
如图所示,半径相同的两个金属小球A、B带有电荷量大小相等的电荷(可视为点电荷),相隔一定的距离,两球之间的相互吸引力大小为F,今用第三个半径相同的不带电的金属小球C先后与A、B两个球接触后移开,这时,A、B两个球之间的相互作用力大小是( )
 如图所示,半径相同的两个金属小球A、B带有电荷量大小相等的电荷(可视为点电荷),相隔一定的距离,两球之间的相互吸引力大小为F,今用第三个半径相同的不带电的金属小球C先后与A、B两个球接触后移开,这时,A、B两个球之间的相互作用力大小是( )
如图所示,半径相同的两个金属小球A、B带有电荷量大小相等的电荷(可视为点电荷),相隔一定的距离,两球之间的相互吸引力大小为F,今用第三个半径相同的不带电的金属小球C先后与A、B两个球接触后移开,这时,A、B两个球之间的相互作用力大小是( )| A. | $\frac{F}{8}$ | B. | $\frac{F}{4}$ | C. | $\frac{3F}{8}$ | D. | $\frac{3F}{4}$ |
 “测定玻璃的折射率”实验中,下图是在纸上留下的实验痕迹,其中直线a、a′是描在纸上的玻璃砖的两个边.
“测定玻璃的折射率”实验中,下图是在纸上留下的实验痕迹,其中直线a、a′是描在纸上的玻璃砖的两个边.