题目内容
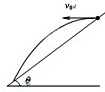 如图,从倾角为θ的斜面上,以速度v0水平抛出质量为m的小球,斜面足够长,空气阻力不计.从小球开始抛出到离开斜面最远的过程中,下列说法正确的是( )
如图,从倾角为θ的斜面上,以速度v0水平抛出质量为m的小球,斜面足够长,空气阻力不计.从小球开始抛出到离开斜面最远的过程中,下列说法正确的是( )分析:当小球的速度方向与斜面平行时,距离斜面最远,根据速度的方向求出运动的时间,从而求出下降的高度,求出重力做的功,根据动能定理求出动能的增加量.
解答:解:A、当小球的速度方向与斜面平行时,距离斜面最远,此时竖直方向上的分速度vy=v0tanθ,则运动的时间t=
=
.故A错误.
B、在这段时间内,物体竖直方向上的位移h=
gt2=
,则重力做功WG=mgh=
m
tan2θ.故B正确.
C、从小球开始抛出到离开斜面最远的过程中,重力做功的功率P=
=
=
.故C错误.
D、根据动能定理,重力做功等于动能的变化,所以动能增加为
m
tan2θ.故D错误.
故选B.
| vy |
| g |
| v0tanθ |
| g |
B、在这段时间内,物体竖直方向上的位移h=
| 1 |
| 2 |
| v02tan2θ |
| 2g |
| 1 |
| 2 |
| v | 2 0 |
C、从小球开始抛出到离开斜面最远的过程中,重力做功的功率P=
| WG |
| t |
| ||||
|
| mv0tanθ |
| 2g |
D、根据动能定理,重力做功等于动能的变化,所以动能增加为
| 1 |
| 2 |
| v | 2 0 |
故选B.
点评:解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,知道当小球的速度方向与斜面平行时,距离斜面最远.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
 一个小球从倾角为37°的斜面上O点以初速v0水平抛出,落在斜面上A点,如图所示,则小球在空中的飞行时间为t=
一个小球从倾角为37°的斜面上O点以初速v0水平抛出,落在斜面上A点,如图所示,则小球在空中的飞行时间为t= 如图所示,从倾角为α=37°的斜面上的A点以速度v0=10m/s平抛一个小球.小球落在斜面上的B点,求:
如图所示,从倾角为α=37°的斜面上的A点以速度v0=10m/s平抛一个小球.小球落在斜面上的B点,求: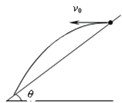 如图,从倾角为θ的斜面上,以速度v0水平抛出质量为m的小球,斜面足够长,空气阻力不计.从小球开始抛出到离开斜面最远的过程中,下列说法不正确的是( )
如图,从倾角为θ的斜面上,以速度v0水平抛出质量为m的小球,斜面足够长,空气阻力不计.从小球开始抛出到离开斜面最远的过程中,下列说法不正确的是( )