题目内容
如图16-4-6所示,在光滑的水平面上有一块质量m=![]()
图16-4-6
(1)如果A、B始终在木板上,两木块间的最大距离.
(2)要使A、B始终在木板上,木板的长度至少要多长?
解析:(1)解法一:两木块在木板上滑动时的加速度为![]() =0.5×
=0.5×
经t s两木块相遇
![]()
t=0.2 s
两木块相遇前瞬间的速度分别为
v1′=
v2′=
两木块相碰后速度交换
v1″=
v2″=
根据动量守恒定律,可求出两木块与木板的共同速度
m2v2″-m1v1″=(m1+m2+m)v
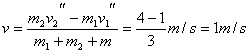
A、B两木块相对静止时相距最远
![]()
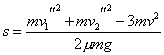
![]()
=
解法二:两木块从开始滑动到相对静止过程中,A、B、C组成的系统动量守恒:
mv1-mv2=(m+m+m)v
从能的转化和守恒来看,减小的机械能全部用来克服摩擦阻力做功转化为热能,且一对摩擦阻力做功的代数和与接触面间的相对滑动的路程有关,令两物体最终相距s,则有
![]()
同理可得:s=
(2)A、B两木块相遇时A向右的位移为sa
![]()
A、B相碰后,A向左的速度减小到零时,向左的位移为sa′
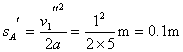
木板的最短长度为d
d=s+sA-sA′=
答案:(1)

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目




