题目内容
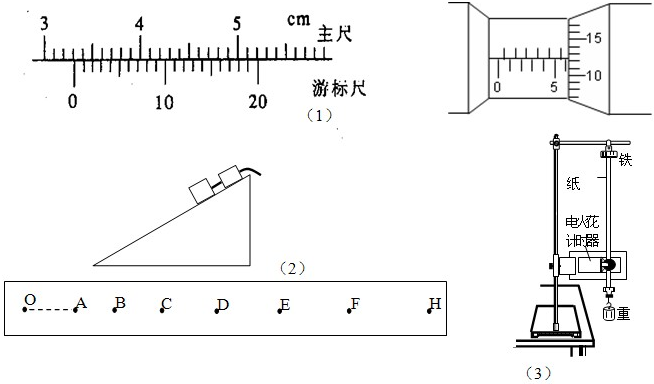
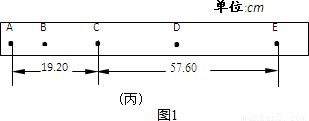
(1)读出下面图1中游标卡尺与螺旋测微器的读数,游标卡尺读数为

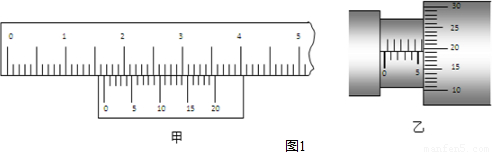
(2)某同学在做验证机械能守恒定律的实验中,使用50Hz交变电流作电源,在打出的纸带上选择5个计数点A、B、C、D、E,相邻两个计数点之间还有4个点没有画出,他测量了C点到A点、和E点到C点的距离,如图1(丙)所示.则纸带上C点的速度vc=

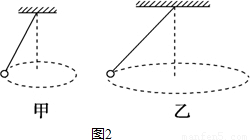
(3)用一根细绳,一端系住一定质量的小球,另一端固定,使小球在水平面内做匀速圆周运动.现有两个这样的装置,如图2,甲和乙所示.已知a,b两小球转动的角速度大小相同,绳与竖直方向的夹角分别为37°和53°.则a、b两小球的转动半径Ra和Rb之比为

16.60
16.60
mm,螺旋测微器读数为5.693 (5.692-5.696)
5.693 (5.692-5.696)
mm.
(2)某同学在做验证机械能守恒定律的实验中,使用50Hz交变电流作电源,在打出的纸带上选择5个计数点A、B、C、D、E,相邻两个计数点之间还有4个点没有画出,他测量了C点到A点、和E点到C点的距离,如图1(丙)所示.则纸带上C点的速度vc=
1.9
1.9
m/s,重物的加速度为9.6
9.6
m/s2.(结果保留两位有效数字)
(3)用一根细绳,一端系住一定质量的小球,另一端固定,使小球在水平面内做匀速圆周运动.现有两个这样的装置,如图2,甲和乙所示.已知a,b两小球转动的角速度大小相同,绳与竖直方向的夹角分别为37°和53°.则a、b两小球的转动半径Ra和Rb之比为
9:16
9:16
.(sin37°=0.6;cos37°=0.8)
分析:(1)游标卡尺读数的方法是主尺读数加上游标读数,不需估读.螺旋测微器的读数方法是固定刻度读数加上可动刻度读数,在读可动刻度读数时需估读;
(2)利用在匀变速直线运动中,中间时刻的瞬时速度等于该过程中的平均速度大小,据此可以求出C点速度大小;利用逐差法可以求出加速度的大小;
(3)小球做圆周运动的向心力由绳子的拉力和重力的合力提供,根据牛顿第二定律求出角速度与半径的关系,从而得出转动半径之比,再根据几何关系得出绳长之比.
(2)利用在匀变速直线运动中,中间时刻的瞬时速度等于该过程中的平均速度大小,据此可以求出C点速度大小;利用逐差法可以求出加速度的大小;
(3)小球做圆周运动的向心力由绳子的拉力和重力的合力提供,根据牛顿第二定律求出角速度与半径的关系,从而得出转动半径之比,再根据几何关系得出绳长之比.
解答:解:(1)游标卡尺的主尺读数为16mm,游标读数为:0.05×12mm=0.60mm,所以最终读数为:16mm+0.60mm=16.60mm;
螺旋测微器固定刻度为5.5mm,可动刻度为:0.01×19.3=0.193mm,所以最终读数为:5.5mm+0.1193mm=5.693mm,由于需要估读,因此在范围5.692-5.696mm都正确.
故答案为:16.60,5.693 (5.692-5.696).
(2)匀变速直线运动中,中间时刻的瞬时速度等于该过程中的平均速度大小,计数点之间的时间间隔为:T=0.1s,所以有:
vC=
≈1.9m/s
根据△x=aT2有:
a=
≈9.6m/s2
故答案为:1.9,9.6.
(3)小球所受的合力F合=mgtanθ=mrω2,则角速度的大小ω=
,
由于角速度大小相等,则转动的半径比Ra:Rb=tan37°:tan53°=9:16.
故答案为:Ra:Rb=9:16.
螺旋测微器固定刻度为5.5mm,可动刻度为:0.01×19.3=0.193mm,所以最终读数为:5.5mm+0.1193mm=5.693mm,由于需要估读,因此在范围5.692-5.696mm都正确.
故答案为:16.60,5.693 (5.692-5.696).
(2)匀变速直线运动中,中间时刻的瞬时速度等于该过程中的平均速度大小,计数点之间的时间间隔为:T=0.1s,所以有:
vC=
| xAE |
| 4T |
根据△x=aT2有:
a=
| xCE-xAC |
| (2T)2 |
故答案为:1.9,9.6.
(3)小球所受的合力F合=mgtanθ=mrω2,则角速度的大小ω=
|
由于角速度大小相等,则转动的半径比Ra:Rb=tan37°:tan53°=9:16.
故答案为:Ra:Rb=9:16.
点评:(1)解决本题的关键掌握游标卡尺读数的方法,主尺读数加上游标读数,不需估读.以及螺旋测微器的读数方法,固定刻度读数加上可动刻度读数,在读可动刻度读数时需估读.
(2)在处理实验打出的纸带时,经常要用匀变速直线运动规律以及去推论,因此要加强基本物理规律在实验中的应用.
(3)解决本题的关键知道小球圆周运动的向心力的来源,根据牛顿第二定律进行求解.
(2)在处理实验打出的纸带时,经常要用匀变速直线运动规律以及去推论,因此要加强基本物理规律在实验中的应用.
(3)解决本题的关键知道小球圆周运动的向心力的来源,根据牛顿第二定律进行求解.

练习册系列答案
相关题目