题目内容
伽利略在研究自由落体运动时,做了如下的实验:他让一个铜球从阻力很小(可忽略不计)的斜面上由静止开始滚下,并且做了上百次。假设某次试验伽利略是这样做的:在斜面上任取三个位置A、B、C,让小球分别由A、B、C滚下,如图所示。设A、B、C与斜面底端的距离分别为s1、s2、s3,小球由A、B、C运动到斜面底端的时间分别为t1、t2、t3, 小球由A、B、C运动到斜面底端时的速度分别为v1、v2、v3,则下列关系式中正确,并且是伽利略用来证明小球沿光滑斜面向下的运动是匀变速直线运动的是( )
A.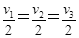 B
B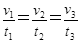
C.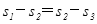 D.
D.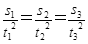
D
解析试题分析:小球在斜面上三次运动的位移不同,末速度一定不同,故A错误;由速度公式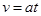 得
得 ,三次下落中的加速度相同,即关系式正确,但并不是当年伽利略用来证明匀变速直线运动的关系,所以B错误;由匀变速直线运动规律及图示可知
,三次下落中的加速度相同,即关系式正确,但并不是当年伽利略用来证明匀变速直线运动的关系,所以B错误;由匀变速直线运动规律及图示可知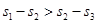 ,所以C错误;由运动学公式
,所以C错误;由运动学公式 可知
可知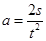 ,所以三次下落中位移与时间平方的比值必为定值,伽利略正是用这一规律证明小球沿光滑斜面向下的运动是匀变速直线运动的,所以D正确;
,所以三次下落中位移与时间平方的比值必为定值,伽利略正是用这一规律证明小球沿光滑斜面向下的运动是匀变速直线运动的,所以D正确;
考点:匀变速直线运动及其公式

物体做匀变速直线运动,下列说法中正确的是( )
| A.第1 s内速度的变化量小于第2 s内速度的变化量 |
| B.第1 s内速度的变化量大于第2 s内速度变化量 |
| C.第1 s内位移小于第2 s内的位移 |
| D.相邻两段相等时间内位移之差等于一个恒量 |
一物体做匀变速直线运动,当t=0时,物体的速度大小为12m/s,方向向东;当t=2s时,物体的速度大小为8m/s,方向仍向东。则物体的速度大小变为2m/s,经过的时间为
| A.3s | B.5s | C.7s | D.9s |
从某高处竖直向上抛出一物体,在5s内该物体通过的路程为65m,若空气阻力不计,则该物体抛出时的速度可能是
| A.20m/s | B.30m/s | C.40m/s | D.60m/s |
在光滑水平面上, 、
、 两小球沿水平面相向运动. 当小球间距小于或等于
两小球沿水平面相向运动. 当小球间距小于或等于 时,受到大小相等、方向相反的相互排斥恒力作用,小球间距大于
时,受到大小相等、方向相反的相互排斥恒力作用,小球间距大于 时,相互间的排斥力为零,小球在相互作用区间运动时始终未接触,两小球运动时速度
时,相互间的排斥力为零,小球在相互作用区间运动时始终未接触,两小球运动时速度 随时间
随时间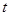 的变化关系图象如图所示,由图可知 ( )
的变化关系图象如图所示,由图可知 ( )
A. 球质量大于 球质量大于 球质量 球质量 |
B.在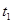 时刻两小球间距最小 时刻两小球间距最小 |
C.在 时间内两小球间距逐渐减小 时间内两小球间距逐渐减小 |
D.在 时间内 时间内 球所受排斥力方向始终与运动方向相反 球所受排斥力方向始终与运动方向相反 |
如图所示,光滑斜面AE被分成四个长度相等的部分,即AB=BC=CD=DE,一物体从A点由静止释放,下列结论中正确的是 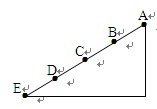
A.物体到达各点的速率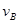 : :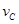 : :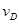 : :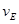 =1: =1: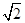 : :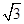 :2 :2 |
B.物体到达各点经历的时间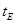 = =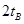 = =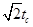 = =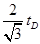 |
C.物体从A 运动到E全过程的平均速度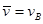 |
D.物体通过每一部分时,其速度增量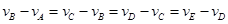 |
做初速度为零的匀加速直线运动的某质点,在第二秒内的位移是6m,那么它在第四秒内的位移是 ( )
| A.8m | B.9m | C.10m | D.14m |
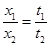
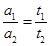
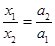
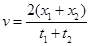
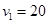 m/s的速率沿平直公路行驶,驾驶员突然发现正前方
m/s的速率沿平直公路行驶,驾驶员突然发现正前方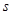 处有一辆汽车.汽车的初速度大小为
处有一辆汽车.汽车的初速度大小为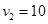 m/s,此时汽车减速的加速度大小为
m/s,此时汽车减速的加速度大小为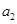 。为了避免发生碰撞,摩托车也同时减速(不计反应时间),求下列各种情况下摩托车减速的加速度大小
。为了避免发生碰撞,摩托车也同时减速(不计反应时间),求下列各种情况下摩托车减速的加速度大小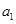 至少为多少?
至少为多少?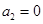 m/s2(即汽车匀速行驶),
m/s2(即汽车匀速行驶),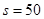 m;
m;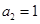 m/s2,
m/s2,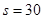 m;
m;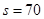 m。
m。