��Ŀ����
6�� ��ͼ��ʾ��·�У����������Ϊ���������պϿ���S��A��A1��V��������Ķ����ֱ�ΪI��I1��U�������߱�������������P������ƶ�һЩ��������������ı仯���ֱ�Ϊ��I����I1����U����˹����У�������
��ͼ��ʾ��·�У����������Ϊ���������պϿ���S��A��A1��V��������Ķ����ֱ�ΪI��I1��U�������߱�������������P������ƶ�һЩ��������������ı仯���ֱ�Ϊ��I����I1����U����˹����У�������| A�� | I��С��I1��С��$\frac{I}{{I}_{1}}$���� | B�� | I��С��I1��С��$\frac{��I}{��{I}_{1}}$���� | ||
| C�� | U���I����$\frac{��U}{��I}$���� | D�� | U���I1����$\frac{��U}{��{I}_{1}}$���� |
���� ������·ͼ��֪����ֵ����R2�뻬��������������������A���·������������A1��ͨ���������ĵ�������ѹ��V��·�˵�ѹ���������������Ļ�ƬP�����ƶ�ʱ�����������������·�ĵ������ݲ�����·�Ĺ��ɺ�ŷķ���ɷ�����
��� �⣺�������������Ļ�ƬP�����ƶ�ʱ�����������������·�ĵ��������·�ܵ������ܵ���I��С����Դ���ڵ�ѹ��С����·�˵�ѹU���ͨ��R2�ĵ���������I1��С��
���ݱպϵ�·ŷķ���� U=E-Ir�ã�$\frac{��U}{��I}$=r�����䣮
��Ϊ��I2=$\frac{��U}{{R}_{2}}$����I=$\frac{��U}{r}$����I=��I1+��I2�������С�I1=��I-��I2=��U��$\frac{1}{r}$-$\frac{1}{{R}_{2}}$��
�ɵ� $\frac{��I}{��{I}_{1}}$=$\frac{{R}_{2}}{{R}_{2}-r}$�����䣮$\frac{��U}{��{I}_{1}}$=$\frac{{R}_{2}r}{{R}_{2}-r}$���䣮��BCD��ȷ��A����
��ѡ��BCD
���� �����ǵ�·��̬�仯�������⣬�������ա��ֲ���������ֲ�����˼·���������ڵ�ѹ������仯�����о����������ݱպϵ�·ŷķ���ɺʹ������������ص���ʽ������

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д� һ������������ڵ糡����ֱ���˶���v-tͼ����ͼ��ʾ��t1��t2ʱ�̷ֱ�M��N���㣬��֪���˶����������ӽ��ܵ糡�����ã��������ж���ȷ���ǣ�������
һ������������ڵ糡����ֱ���˶���v-tͼ����ͼ��ʾ��t1��t2ʱ�̷ֱ�M��N���㣬��֪���˶����������ӽ��ܵ糡�����ã��������ж���ȷ���ǣ�������| A�� | �ڴ�M�㵽N��Ĺ����У������������� | |
| B�� | M��ĵ��Ƶ���N��ĵ��� | |
| C�� | �õ糡��������ij�������γɵ� | |
| D�� | ����������M�����ܵ糡��С����N�����ܵ糡�� |
 ��ͼ��ʾ����鱻�������ʵ���ˮƽ��ס���ھ�ֹ״̬����֪�������Ϊ100N����ˮƽ���������Ħ����Ϊ42N����Ħ��������=0.4������A������Ϊ50N������B������Ϊ30N��
��ͼ��ʾ����鱻�������ʵ���ˮƽ��ס���ھ�ֹ״̬����֪�������Ϊ100N����ˮƽ���������Ħ����Ϊ42N����Ħ��������=0.4������A������Ϊ50N������B������Ϊ30N��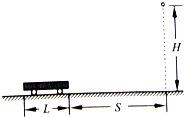 ��ͼ��ʾ���ڹ⻬ˮƽ��������һ����ΪL=10m��С������ʹС���Գ��ٶ�v0����������ֱ���˶������ٶ�Ϊa=2m/s2�����ͬʱ��С������ǰ��S=48m�������Ϸ�H=20m�ߴ�����һ������Ϊ�ʵ��С���ɾ�ֹ��ʼ�����������˶�������С���߶ȣ��������ٶ�g=10m/s2��ҪʹС�����䵽С���ϣ�С���ij��ٶ�v0Ӧ����ʲô������
��ͼ��ʾ���ڹ⻬ˮƽ��������һ����ΪL=10m��С������ʹС���Գ��ٶ�v0����������ֱ���˶������ٶ�Ϊa=2m/s2�����ͬʱ��С������ǰ��S=48m�������Ϸ�H=20m�ߴ�����һ������Ϊ�ʵ��С���ɾ�ֹ��ʼ�����������˶�������С���߶ȣ��������ٶ�g=10m/s2��ҪʹС�����䵽С���ϣ�С���ij��ٶ�v0Ӧ����ʲô������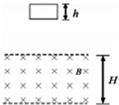 ��ͼ��ʾ���Ը��Ծ���ͭ����Ȧ��ijһ�ߴ��������䣬����һ��ˮƽ���н���ǿ�ų�����Ȼ���ų�������ֱ��������Ȧ�ij���hС�ڴų��ij���H���˶���������Ȧƽ��ʼ������ֱƽ�����Ҳ�����ת��������P-xͼ���ܶ��Ա�ʾ��Ȧ��ͨ���ų������ɸ�Ӧ�����Ĺ���P������λ��x�仯���ǣ�������
��ͼ��ʾ���Ը��Ծ���ͭ����Ȧ��ijһ�ߴ��������䣬����һ��ˮƽ���н���ǿ�ų�����Ȼ���ų�������ֱ��������Ȧ�ij���hС�ڴų��ij���H���˶���������Ȧƽ��ʼ������ֱƽ�����Ҳ�����ת��������P-xͼ���ܶ��Ա�ʾ��Ȧ��ͨ���ų������ɸ�Ӧ�����Ĺ���P������λ��x�仯���ǣ�������
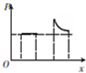

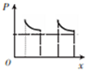
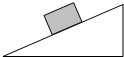 ��ͼ��ʾ��һ����Ϊ5N�����徲ֹ����б��Ϊ30��Ĵֲ�б���ϣ��������ܵ���б�����ϵ�3N��Ħ������4N��֧��������
��ͼ��ʾ��һ����Ϊ5N�����徲ֹ����б��Ϊ30��Ĵֲ�б���ϣ��������ܵ���б�����ϵ�3N��Ħ������4N��֧�������� ��ͼ��ʾ��8����ȫ��ͬ��ľ������ž�����ˮƽ�����ϣ�ÿ��ľ������Ϊm=0.2kg������l=1.0m��ľ�������䶯Ħ��������=0.2������һС��飨����Ϊ�ʵ㣩��ˮƽ���ٶ�v0=$\sqrt{57}$m/s�ӡ�1����ľ��������ľ�壬С�������M=0.5kg��С�����ľ��䶯Ħ��������2=0.4��ȡ�������ٶ�g=10m/s2����
��ͼ��ʾ��8����ȫ��ͬ��ľ������ž�����ˮƽ�����ϣ�ÿ��ľ������Ϊm=0.2kg������l=1.0m��ľ�������䶯Ħ��������=0.2������һС��飨����Ϊ�ʵ㣩��ˮƽ���ٶ�v0=$\sqrt{57}$m/s�ӡ�1����ľ��������ľ�壬С�������M=0.5kg��С�����ľ��䶯Ħ��������2=0.4��ȡ�������ٶ�g=10m/s2����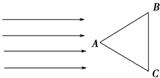 �������εIJ���ש����ͼ13��ʾ���ã������Ϊ�߳�Ϊl�ĵȱ������Σ�һ������Ϊl�ĵ�ɫƽ�й������Դ�ֱ��BC��ķ������öԳƵ����䵽�ò���ש��AB��AC���ϣ�������д�AB��AC������Ĺ��߽����ǡ��ȫ��ֱ�ӵ���BC�棬��BC����������䵽ƽ����BC��Ĺ����ϣ�
�������εIJ���ש����ͼ13��ʾ���ã������Ϊ�߳�Ϊl�ĵȱ������Σ�һ������Ϊl�ĵ�ɫƽ�й������Դ�ֱ��BC��ķ������öԳƵ����䵽�ò���ש��AB��AC���ϣ�������д�AB��AC������Ĺ��߽����ǡ��ȫ��ֱ�ӵ���BC�棬��BC����������䵽ƽ����BC��Ĺ����ϣ�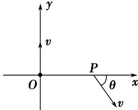 ��xOyƽ������OΪԲ�ġ��뾶Ϊr��Բ�������ڣ����ڴŸ�Ӧǿ��ΪB����ǿ�ų����ų�����ֱ��xOyƽ�棬һ������Ϊm�������Ϊq�Ĵ������ӣ���ԭ��O��ijһ���ٶ�v0��y��������ʼ�˶���һ��ʱ���x���ϵ�P�㣬��ʱ�ٶ���x�᷽��нǦ�=30�㣬��ͼ��ʾ������������Ӱ�죬��
��xOyƽ������OΪԲ�ġ��뾶Ϊr��Բ�������ڣ����ڴŸ�Ӧǿ��ΪB����ǿ�ų����ų�����ֱ��xOyƽ�棬һ������Ϊm�������Ϊq�Ĵ������ӣ���ԭ��O��ijһ���ٶ�v0��y��������ʼ�˶���һ��ʱ���x���ϵ�P�㣬��ʱ�ٶ���x�᷽��нǦ�=30�㣬��ͼ��ʾ������������Ӱ�죬��