题目内容
【题目】如图(a)所示，在xOy平面内，坐标原点O处有粒子源，沿y轴正方向发射质量为m,电荷量为q(q>0)、初速度为v0的粒子。在y=d处放置足够长、平行于x轴的收集板,不考虑粒子打到板上反弹和粒子间的相互作用，粒子重力忽略不计。
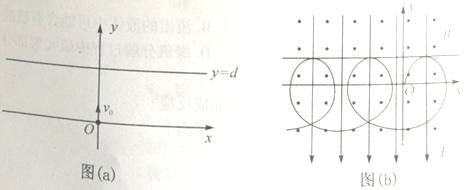
(1)若只在xOy平面内施加沿y轴正向、电场强度为E1的匀强电场，求粒子打在收集板上的速度大小
;
(2)若只在xOy平面内施加垂直纸面向外、磁感应强度为B的匀强磁场(且
),求粒子打在收集板上的位置的横坐标x1;
(3)在第(2)问的前提下，若在xOy平面内加上沿y轴负方向的电场强度大小为E2的匀强电场，使粒子刚好不打在收集板上，轨迹如图(b)所示。研究表明：粒子在xOy平面内做周期性运动，可看作沿轴负方向的匀速直线运动和xOy平面内的匀速圆周运动。求运动过程中的最小速度v和E2的大小。
【答案】（1）
（2）
（3）
【解析】(1)施加电场E1，粒子打到收集板上，由动能定理 
①
解得 ②
(2)沿y轴正向入射的粒子运动轨迹如图所示，打在收集板上的位置A，洛伦兹力提供向心力
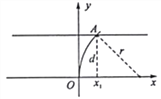
③
又
④
解得 ⑤
(3)v0可分解成如图所示的速度v1、v2，
⑥
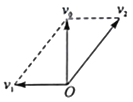
分速度v1对应的洛伦兹力与电场力平衡，
⑦
粒子到最高点时的速度最小
⑧
从坐标原点到最高点，由动能定理
⑨
解得 
⑩
所以
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
