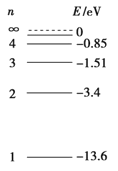
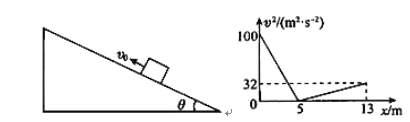
题目内容
【题目】如图所示,一颗质量为m=0.1kg的子弹以v0=50m/s的水平速度打入静止在光滑水平面上质量为M=0.9kg的木块中,并随木块一起沿半径R=![]() m光滑半圆轨道AB运动到最高点B,然后又落回地面。(g取10 m/s2,可把木块与子弹视为质点)
m光滑半圆轨道AB运动到最高点B,然后又落回地面。(g取10 m/s2,可把木块与子弹视为质点)
(1)木块经轨道最高处B点时,对轨道的压力多大。
(2)木块落回水平面时,落地点距A点的距离。

【答案】(1)木块对轨道的压力为61.1N;(2)X=1.2m
【解析】
(1)以子弹与木块组成的系统为研究对象,系统动量守恒,以子弹的初速度方向为正方向。设碰完后共同速度为v1 则有:
mv0=(m+M)v1
得v1=5m/s
对系统从A-B的过程应用动能定理,设在B点的速度为v2 则有
![]()
得![]() =4m/s
=4m/s
对系统在最高点B进行受力分析,应用牛顿第二定律则有:
![]()
得![]() =61.1N (或550/9N)
=61.1N (或550/9N)
由牛顿第三定律可知木块对轨道的压力为61.1N
(2)设木块平抛运动到地面的时间为t,由平抛运动的知识有
![]()
![]()
得X=1.2m

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目