题目内容
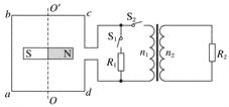
【题目】如图甲，在水平桌面上固定着两根相距L＝20 cm、相互平行的无电阻轨道P、Q，轨道一端固定一根电阻R＝0.02 Ω 的导体棒a，轨道上横置一根质量m＝40 g、电阻可忽略不计的金属棒b，两棒相距也为L＝20 cm。该轨道平面处在磁感应强度大小可以调节的竖直向上的匀强磁场中。开始时，磁感应强度B0＝0.1 T。设棒与轨道间的最大静摩擦力等于滑动摩擦力，g取10 m/s2。
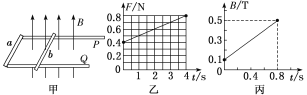
(1)若保持磁感应强度B0的大小不变，从t＝0时刻开始，给b棒施加一个水平向右的拉力，使它由静止开始做匀加速直线运动。此拉力F的大小随时间t变化关系如图乙所示。求b棒做匀加速运动的加速度及b棒与轨道间的滑动摩擦力大小；
(2)若从t＝0开始，无拉力F的作用，磁感应强度B随时间t按图丙中图像所示的规律变化，b棒与轨道间摩擦因数与（1）问中相同，求在金属棒b开始运动前，这个装置释放的热量。
【答案】（1）
，
（2）
【解析】
试题（1）根据安培力和法拉第电磁感应定律：
，
，
所以：
当
棒匀加速运动时，根据牛顿第二定律有：
联立可得：
由图象可得：当
时，
当
时，
可解得，。
（2）当磁感应强度均匀增大时，闭合电路中有恒定的感应电流I，以b棒为研究对象，它受到的安培力逐渐增大，静摩擦力也随之增大，当磁感应度增大到b所受安掊力F/安与最大静摩擦力f相等时开始滑动。
感应电动势：
，
棒将要运动时，有
， 所以：
根据
， 得
回路中产生焦耳热为
练习册系列答案
名校课堂系列答案
相关题目
