题目内容
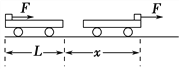
【题目】如图所示,光滑固定的竖直杆上套有一个质量m=0.4 kg的小物块A,不可伸长的轻质细绳通过固定在墙壁上、大小可忽略的定滑轮D,连接小物块A和小物块B,虚线CD水平,间距d=1.2 m,此时连接小物块A的细绳与竖直杆的夹角为37°,小物块A恰能保持静止。现在在小物块B的下端挂一个小物块Q(未画出),小物块A可从图示位置上升并恰好能到达C处.不计摩擦和空气阻力,cos 37°=0.8、sin 37°=0.6,重力加速度g取10 m/s2,下列正确的是( )
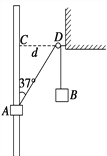
A. 小物块A到达C处时的加速度为g
B. 小物块A到达C处时的加速度为0
C. 小物块B的质量0.5kg
D. 小物块Q的质量0.3kg
【答案】ACD
【解析】当A物块到达C处时,由受力分析可知:水平方向受力平衡,竖直方向只受重力作用,所以A物块的加速度a=g;选项A正确,B错误;B物体受重力和拉力而平衡,故拉力等于其重力;物体A受重力、拉力和杆的支持力,如图所示;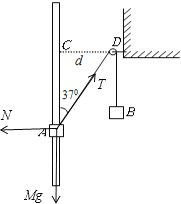
设B物块的质量为M,绳子拉力为T;根据平衡条件:Tcos37°=mg;T=Mg;联立解得M=0.5kg;设Q物块的质量为mo,根据系统机械能守恒得:mghac=(M+mo)ghb;hac=dcot37°=1.6m;hb=![]() d=0.8m;解得:mo=0.3kg,选项CD正确;故选ACD.
d=0.8m;解得:mo=0.3kg,选项CD正确;故选ACD.

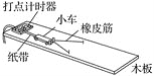
【题目】橡皮筋也像弹簧一样,在弹性限度内,伸长量x与弹力F成正比,即F=kx,k的值与橡皮筋未受到拉力时的长度L、横截面积S有关,理论与实践都表明k=YS/L,其中Y是一个由材料决定的常数,材料力学中称之为杨氏模量.

(1)有一段横截面是圆形的橡皮筋,应用如图甲所示的实验装置可以测量出它的杨氏模量Y的值.下表为橡皮筋受到的拉力F与伸长量x的实验记录,请在图乙中作出F-x图象_____.
拉力F/N | 5.0 | 10.0 | 15.0 | 20.0 | 25.0 |
伸长量x/cm | 1.60 | 3.20 | 4.80 | 6.40 | 8.00 |
(2)由以上实验可求出该橡皮筋的K值为________N/m(保留两位有效数字).

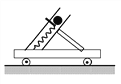
(3)某同学在家中用三根相同的橡皮筋(遵循胡克定律)来探究合力的方法,如图所示,三根橡皮筋在O点相互连接,拉长后三个端点用图钉固定在A、B、C三点.在实验中,可以通过刻度尺测量橡皮筋的长度来得到橡皮筋的拉力大小,并通过OA、OB、OC的方向确定三个拉力的方向,从而探究求其中任意两个拉力的合力的方法.在实验过程中,下列说法正确的是(____)
A.只需要测量橡皮筋的长度,不需要测出橡皮筋的原长
B.为减小误差,应选择劲度系数尽量大的橡皮筋
C.以OB、OC为两邻边作平行四边形,其对角线必与OA在一条直线上且长度与OA相等
D.多次实验中即使O点不固定,也可以探究求合力的方法